Виды и формы средних
Значение средней зависит от того, каков порядок ее расчета. Средние применяются двух видов: простые и взвешенные.
Простая средняя получается путем деления суммы значений на их количество.
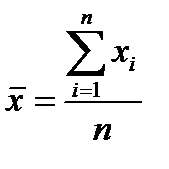
Пример. Заработная плата за февраль у трех рабочих одного цеха составила: 6 600 руб., 4 960 руб., 5 320 руб.
Средняя заработная плата за месяц составит
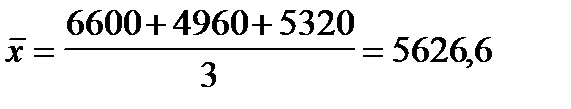 руб.
руб.
Такая средняя называется простой средней арифметической.
Характер данных может повлиять на порядок расчета средней.
Пример. По каждому из трех рабочих, которые делают одну и ту же операцию, известно следующее (табл. 3.1).
Таблица 3.1.
| Рабочие | Число деталей, изготовленных за 1 час работы | Количество отработанных часов за месяц |
| 1-й | ||
| 2-й | ||
| 3-й |
Тогда:
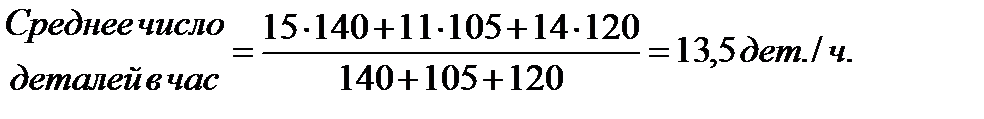
Таким образом, в расчете средней часовой выработки рабочих участвовали не только данные о часовой выработке каждого из них, но и количество отработанных часов.
Проделанный расчет средней можно записать в виде формулы.
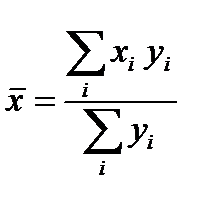 ,
,
где 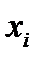 — часовая выработка i-го рабочего;
— часовая выработка i-го рабочего;
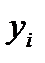 — количество часов, отработанных i-м рабочим за месяц.
— количество часов, отработанных i-м рабочим за месяц.
Такая средняя называется арифметической взвешенной. В данном примере 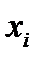 (часовая выработка) — усредняемый признак;
(часовая выработка) — усредняемый признак; 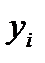 (количество отработанных часов) — признак-вес. Умножая
(количество отработанных часов) — признак-вес. Умножая 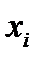 на
на 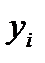 , мы производим взвешивание, которое позволяет учесть значимость часовой выработки каждого рабочего для расчета средней часовой выработки.
, мы производим взвешивание, которое позволяет учесть значимость часовой выработки каждого рабочего для расчета средней часовой выработки.
Представим, что мы не будем учитывать количество отработанных часов, и найдем среднюю выработку как простую арифметическую
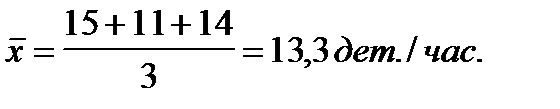
Т.е. результат хотя и незначительно, но отличается от того, который получен при использовании средней взвешенной.
Чем значительнее неравенство весов и чем сильнее признак-вес связан с усредняемым признаком, тем большее значение взвешенной средней отличается от простой средней.
Все средние, используемые в статистических расчетах, относятся к степенным средним. Формула степенной средней в общем виде записывается следующим образом:
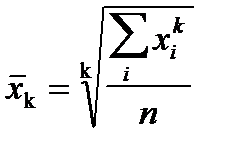 .
.
Вид средней зависит от показателя степени. При k = 1 имеем среднюю арифметическую:
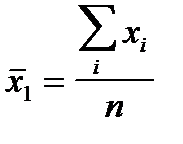 ,
,
при k = 2 — среднюю квадратическую:
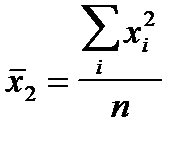 ,
,
при k = 0 — среднюю геометрическую
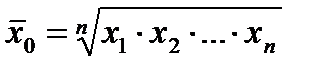 ,
,
при k = -1 — среднюю гармоническую
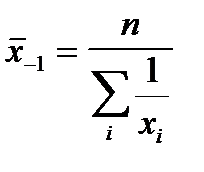 .
.
Основной формой средних является средняя арифметическая. Ее формула прямо отвечает определению средней величины как обобщенной характеристики единицы совокупности.
Подчеркнем, что важнейшим условием определения достоверности средних величин является однородность изучаемой совокупности. Нарушение этого требования приводит к появлению фиктивных средних, искажающих статистические выводы.
Совокупность считается однородной, если все составляющие ее единицы относятся к одному и тому же типу складывающихся под влиянием общих, систематически действующих факторов.
Вопросы для самоконтроля
1. Что такое средние величины?
2. Чем определяется особая роль средних величин?
3. Каковы факторы надежности средних величин?
4. Какие операции включает расчет средней величины?
5. В чем отличие простой средней от арифметической взвешенной?
6. Какова формула степенной средней?
7. В каком случае совокупность считается однородной?
Глава 4. Вариация
Дата добавления: 2016-05-16; просмотров: 1191;
