Начальная остойчивость

Малые равнообъемные наклонения

Теорема Эйлера

Одним из двух положений (допущений) метода начальной остойчивости является теорема Эйлера о равнообъемных ватерлиниях.

Теорема гласит, что линия пересечения равнообъемных ватерлиний при бесконечно малом угле наклонения проходит через центры тяжести площадей начальной и конечной ватерлиний.

Для доказательства этой теоремы рассмотрим наклонение судна вокруг продольной оси на правый борт (рис. 2.1). На рис. 2.1 принято: наклонение судна происходит на бесконечно малый угол (dq) при сохранении прямостенности корпуса; ВЛ₀, ВЛ₁ – след начальной и конечной (после наклонения) ватерлиний соответственно; dV₁, dV₂ – объем клина водоизмещения вошедшего в воду и вышедшего из воды соответственно. Из условия равнообъемного наклонения имеем dV₁ = dV₂.

Рис. 2.1. К доказательству теоремы Эйлера

Предположим, что следы плоскостей начальной и конечной ватерлинии пересекаются в точке 0. С учетом того, что угол наклонения бесконечно мал, тангенс угла и его значение в радианах можно принять равными.

Приняв во внимание начальную ватерлинию ВЛ₀, объем клина, вошедшего в воду по всей длине корпуса (от – L/2 до + L/2), можно представить в виде

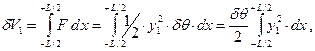
где		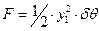–	площадь сечения клина;
	dx	–	элемент длины корпуса судна;
	dq	–	постоянный по длине корпуса угол.

Аналогично можно получить выражение для вышедшего из воды клина водоизмещения

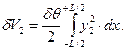
(2.1)

Из равенства объемов клиньев, вошедшего и вышедшего из воды, получаем следующее условие равнообъемного наклонения

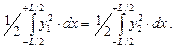
Правая и левая части этого равенства представляют собой статический момент части площади ватерлинии, расположенной по одну сторону от оси «х», поскольку 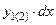есть элементарная площадка, а 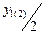– расстояние от центра ее тяжести до оси «х» (рис. 2.2).

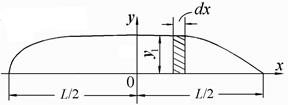
Рис. 2.2. К определению статического момента площади ватерлинии

Статические моменты двух частей площади любой фигуры относительно оси, разбивающей фигуру на эти части, равны только тогда, когда ось проходит через центр тяжести площади фигуры. Поскольку статические моменты двух частей площади начальной ватерлинии равны, то ось, относительно которой они взяты, проходит через центр тяжести площади начальной ватерлинии. Повторив эти рассуждения для ВЛ₁ можно получить такой же вывод и для конечной ватерлинии.

Таким образом, линия пересечения двух равнообъемных ватерлиний при бесконечно малом наклонении проходит через центры тяжести обеих ватерлиний. Теорему Эйлера распространяют и на конечные, но малые углы наклонения. На практике к малым углам наклонения относят углы до 7–10°. Теорема Эйлера выполняется при наклонениях в пределах прямостенности бортов (рис. 2.1).

Углы наклонения судов в продольной вертикальной плоскости (углы дифферента), как правило, не превышают 7°. При продольном наклонении след конечной ватерлинии будет пересекаться со следом начальной ватерлинии в точке F – в центре тяжести начальной ватерлинии (рис. 2.3).

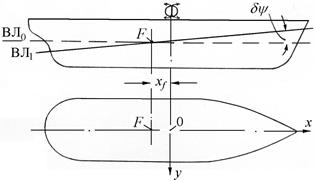
Рис. 2.3. Положение равнообъемных ватерлиний при дифференте

Поперечная ось, проходящая через точку F, в этом случае будет осью вращения судна.