Составляющие дифференциального уравнения колебаний управляемого колеса.
 Во время колебаний управляемого колеса относительно оси шкворня действуют следующие моменты: возмущающий момент от дисбанса колеса, момент сопротивления повороту шины, упругий момент в рулевом управлении, стабилизирующий момент шины, катящегося с уводом управляемого колеса, весовой и скоростной стабилизирующие моменты, момент от продольных сил, гироскопический и инерционный моменты и момент трения в шкворневом узле автомобиля.
Во время колебаний управляемого колеса относительно оси шкворня действуют следующие моменты: возмущающий момент от дисбанса колеса, момент сопротивления повороту шины, упругий момент в рулевом управлении, стабилизирующий момент шины, катящегося с уводом управляемого колеса, весовой и скоростной стабилизирующие моменты, момент от продольных сил, гироскопический и инерционный моменты и момент трения в шкворневом узле автомобиля.
Возмущающий момент от дисбаланса управляемого колеса.
Схема для определения возмущающего момента, вызванного дисбалансом управляемого колеса, приведена на рис. 9.15.
Рис.9.15 Схема для определения возмущающего момента
Пусть управляемое колесо имеет приведенную массу дисбаланса D m, расположенную относительно оси цапфы на расстоянии Rg и относительно оси шкворня на расстоянии D l (см. рис. 9.15).
При вращении колеса с угловой скоростью wк возникает центробежная сила 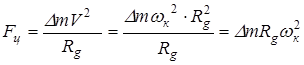 .
.
Относительно оси шкворня эта центробежная сила вызовет возмущающий момент, равный
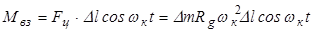 . (9.41)
. (9.41)
Этот возмущающий момент, воздействуя на управляемое колесо, вызывает при определенных условиях колебания управляемого колеса
Поскольку колесо при колебании поворачивается относительно оси шкворня с угловой скоростью  , поэтому возникает момент сопротивления повороту шины, который с учетом изложенного выше равен
, поэтому возникает момент сопротивления повороту шины, который с учетом изложенного выше равен
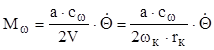 , (9.42)
, (9.42)
где rк – радиус колеса.
Во время колебаний автомобиль не изменяет траекторию своего движения, а поэтому при колебании колесо катится с переменным углом увода, равным углу колебания колеса. Это вызывает стабилизирущий момент шины. Учитывая, что амплитуда колебаний не превышает 2°, стабилизирующий момент шины определяется по формуле
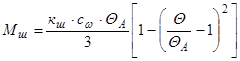 . (9.43)
. (9.43)
При небольшой амплитуде колебаний с достаточной для практики точностью зависимость стабилизирующего момента шины от угла колебаний представим условно линейной и запишем в виде
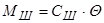 , (9.44)
, (9.44)
где Сш – коэффициент стабилизирующего момента шины, который определяется по формуле
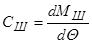 .
.
Взяв производную с выражения (9.43), определим этот коэффициент
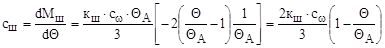 .
.
Во время колебаний водитель удерживает рулевое колесо в неподвижном состоянии. В этом случае возникает закручивание управляемого колеса относительно рулевого, вызывая упругий момент в рулевом управлении, равный
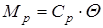 ,
,
где ср – жесткость рулевого управления в Н м/град., которая определяется экспериментально, согласно рис.9.16.

Рис. 9.16 Схема для определения жесткости рулевого управления
При поддомкраченом левом управляемом колесе, снятой поперечной тяге, зафиксированном в неподвижном состоянии рулевом колесе, прикладывается к колесу моментМ=Рl .Одновременно фиксируется угол поворота колеса.
Тогда экспериментально замеренная жесткость рулевого управления относительно оси шкворня левого управляемого колеса равна
 , (9.45)
, (9.45)
где М-приложенный к колесу момент;
 -замеренный угол поворота колеса.
-замеренный угол поворота колеса.
Кроме отмеченных выше моментов, при колебании относительно оси шкворня возникают дополнительно еще четыре момента:
весовой стабилизирующий Мст; скоростной МРб; момент от равнодействующей продольных сил, действующих на колесо МРn; гироскопический момент Мгир.
Анализ приведенных автором в докторской диссертации исследований показал, что эти моменты являются функцией угла продольного наклона шкворня. Их влияние в процессе колебаний учитывается произведением коэффициента дополнительной жесткости управляемого колеса и амплитуды колебаний
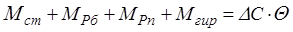 , (9.46)
, (9.46)
где DС –дополнительная жесткость управляемого колеса.
Поскольку эти моменты являются функцией угла продольного наклона шкворня, поэтому величину этого коэффициента рекомендуется определять по эмпирической зависимости 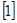
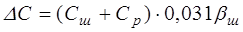 , (9.47)
, (9.47)
где bш – угол продольного наклона шкворня в град.
Препятствовать колебаниям управляемого колеса будет момент трения в подшипниках шкворневого узла, который всегда будет направлен противоположно возмущающему моменту. Что касается моментов трения в рулевом механизме и рулевом приводе, то из-за наличия продольной тяги, имеющей определенную упругость, их влияние на устойчивость колес против колебаний, как показал анализ проведенных, несущественно.
 Поскольку колебания управляемого колеса относительно оси шкворня происходят с угловым ускорением
Поскольку колебания управляемого колеса относительно оси шкворня происходят с угловым ускорением 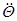 , поэтому возникает инерционный момент.
, поэтому возникает инерционный момент.
 , (9.48)
, (9.48)
где 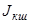 - момент инерции управляемого колеса относительно оси шкворня.
- момент инерции управляемого колеса относительно оси шкворня.
Рис. 9.17 Схема для определения
момента инерции управляемого колеса относительно оси шкворня
Определяется он экспериментально подвешиванием двух спаренных колес на упругой струне (сталь 65Г, Æ 14¸18 мм), согласно рис.9.17. Значения таких моментов инерции для большегрузных автомобилей КамАЗ-5511 и КрАЗ-260 приведены в табл.9.1.
Таблица 9.1 Моменты инерции колес относительнео осей шкворней
| № | Наименование | Масса в кг | Момент инерции в кг.м2 |
| Управляемое колесо КамАЗ-5511 со ступицей в сборе | 184,6 | 10, 39 | |
| Управляемое колесо КрАЗ-260 со ступицей в сборе | 361,15 | 48,32 |
С учетом изложенного уравнение моментов относительно шкворня при колебании управляемого колеса запишется так
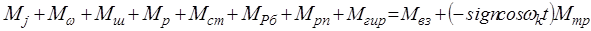 (9.49).
(9.49).
Заметим, что момент трения в шкворневом узле Мтр имеет направление, противоположное вектору возмущающего момента Мвз .Это направление действия момента учитывается соответствующим знаком.
После подстановки значимости составляющих моментов уравнение (9.49) примет вид
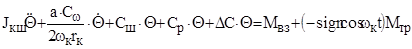 . (9.50)
. (9.50)
После преобразований имеем
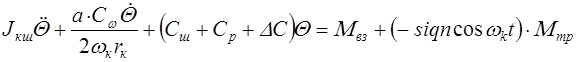 .
.
Введем обозначение 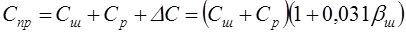 ,
,
где Cпр – приведенная жесткость управляемого колеса.
Окончательно дифференциальное уравнение колебаний управляемого колеса запишется
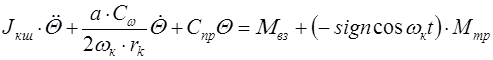 . (9.51)
. (9.51)
Уравнение (9.51) является неоднородным дифференциальным уравнением второго порядка. Его общее решение запишем
 , (9.52)
, (9.52)
где  - общее решение однородного дифференциального уравнения;
- общее решение однородного дифференциального уравнения;
 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
Однородное уравнение запишем
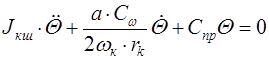 , (9.53)
, (9.53)
или  .
.
Если учесть, что круговая частота соответственных колебаний системы при отсутствии демпфирования равна 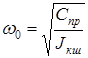 ,
,
тогда имеем
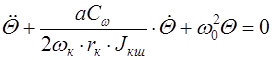 . (9.54)
. (9.54)
Воспользуемся разработками И.А. Вишнеградского (1878 г.)
Введем безразмерное, время 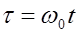 .
.
Тогда имеем 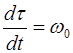
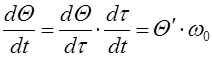
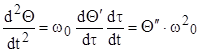 .
.
После подстановки в уравнение (9.54) имеем
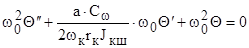 ,
,
или 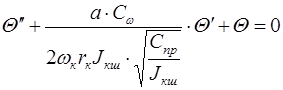 .
.
Уравнение запишем следующим образом
 ,
,
где 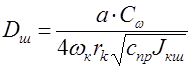 . (9.55)
. (9.55)
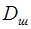 назовем безразмерным коэффициентом демпфирования шины. Этот коэффициент учитывает демпфирующие свойства шины, которые обусловлены моментом сопротивления ее повороту при колебании колеса.
назовем безразмерным коэффициентом демпфирования шины. Этот коэффициент учитывает демпфирующие свойства шины, которые обусловлены моментом сопротивления ее повороту при колебании колеса.
Из формулы (9.55) определим 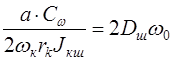
и подставим в уравнение (9.54). В результате имеем
 . (9.56)
. (9.56)
Общее решение уравнения (9.56) будем искать в виде 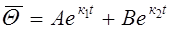 ,
,
где к1, к2 – корни характеристического уравнения. Определим их
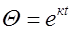 ;
;  ;
; 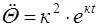 .
.
После подстановки в уравнение (9.56 ), имеем
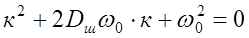 .
.
Отсюда 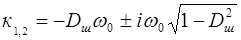
Тогда общее решение однородного дифференциального уравнения запишется
 .
.
Воспользуемся преобразователем Эйлера
 .
.
Тогда общее решение однородного дифференциального уравнения будет
 .
.
Определим коэффициенты с1 и с2 , задавшись начальными условиями:
1. При 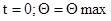 ;
;
2. При 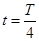 ;
; 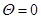 ( Т – период колебаний ).
( Т – период колебаний ).
При t=0 имеем
 . Отсюда
. Отсюда 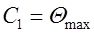 .
.
При 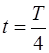 ; T=
; T= 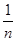 (n – частота собственных колебаний системы)
(n – частота собственных колебаний системы)
 ;
; 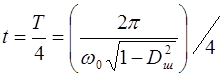 =
= 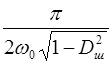 .
.
После подстановки этих условий в уравнение имеем
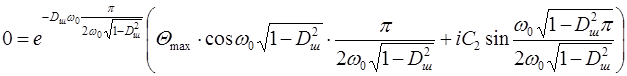 ,
,
или 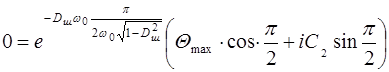 . (9.57)
. (9.57)
Условие уравнения (9.57) будет выполняться при с2=0.
Тогда общее решение однородного дифференциального уравнения запишем
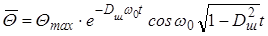 (9.58)
(9.58)
 На рис.9.18 приведен график функции
На рис.9.18 приведен график функции 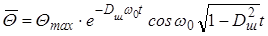 .
.
Рис. 9.18 График функции 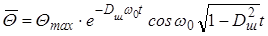
Из анализа рис.9.18 следует, что общее решение однородного дифференциального уравнения представляет затухающую функцию.
Определим частное решение неоднородного уравнения. Поскольку правая часть уравнения не является функцией угла колебаний управляемого колеса, поэтому решение будем искать в виде
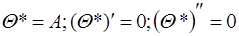 .
.
После подстановки этих значений в уравнение (9.51), имеем
 .
.
Отсюда 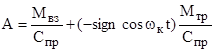 .
.
Тогда общее решение неоднородного дифференциального уравнения запишется
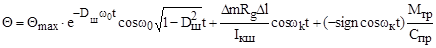 . (9.59)
. (9.59)
Определим условия отсутствия колебаний управляемого колеса. Для этого в уравнении(9.59) приравняем угол колебаний 
 .
.
Условие уравнения будет выполняться, если
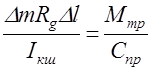 .
.
Введем понятие предельный против колебаний момент трения в шкворневом узле, под которым будем понимать минимальный момент трения, обеспечивающий устойчивость колес против колебаний. Из анализа вышеприведенной зависимости следует
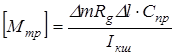 , (9.60)
, (9.60)
где 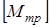 - предельный против колебаний момент трения в шкворневом узле. Если момент трения в шкворневом узле окажется меньше предельного по
- предельный против колебаний момент трения в шкворневом узле. Если момент трения в шкворневом узле окажется меньше предельного по
устойчивости против колебаний, рассчитанного по формуле (9.60), то наступают колебания колес.
Из существующих конструкций шкворневых узлов наиболее склонны к колебаниям конструкции полноприводных автомобилей. В шкворневых узлах этих автомобилей установлены конические радиально-упорные подшипники. При эксплуатации автомобилей изнашиваются ролики и обоймы подшипников, уменьшается их преднатяг а значит уменьшается и момент трения в шкворневых узлах этих автомобилей. Если его величина становится меньше предельного по устойчивости против колебаний момента трения, то наступают колебания управляемых колес.
Что же касается гироскопического эффекта, возникающего при колебании управляемых колес, то он является следствием колебаний, вызванных дисбалансом, но никак не источником колебаний.
Литература
1.Солтус А.П. Основы теории рабочего процесса и расчета колесных управляющих модулей (монография). Деп.Укр.НИИНТИ.№501-Ук90 ВИНИТИ «Деп.науч.труды»,1990, №7 (290),б/о 203.-234с., с.-58..67, 171-192.
2.Литвинов А.С., Фаробин Я.Е. Автомобиль: Теория эксплуатационных свойств.-М.: Машиностроение, 1984.-272 с., с.-150…158
3.Солтус А.П., Барун В.Н., Азаматов Р.А. Влияние характеристик элементов рулевого управления на «шимми» управляемых колес автомобиля. Ж. Автомобильная промышленность.-М.,1985.-№2.
4 Солтус А.П.,Азаматов Р.А. Шкворневые узлы автомобилей большой грузоподъемности. Ж. Автомобильная промышленность.-М., 1986.-№11.
Контрольные вопросы
1.Перечислите источники, вызывающие колебания управляемых колес автомобилей?
2..Чем вызван возмущающий момент ?
3. В каких одновременно двух движениях участвует шина во время колебаний?
4. Что вызывает поворот колеса относительно оси шкворня при колебаниях?
5. С каким углом увода катится управляемое колесо при колебаниях?
6. Чем обусловлена приведенная жесткость управляемого колеса?
7. Что такое предельный против колебаний момент трения в шкворневом узле автомобиля?
8. Перечислите факторы, что влияют на величину предельного против колебаний момента трения в шкворневом узле автомобиля?
9. Почему колебания управляемых колес имеют место на полноприводных автомобилях?
10. Какие функции выполняет момент трения в шкворневых узлах автомобилей?
11. В каком случае наступают колебания управляемых колес?
Дата добавления: 2016-05-11; просмотров: 1347;
