Понятие неоднородности. Примеры. Характеристики неоднородностей.

В бесконечной, однородной, изотропной среде, свойства которой неизменны по всем направлениям и на любых расстояниях от источ­ника, отражений не бывает. Отражения появляются, когда есть неодно­родности в среде. Неоднородности среды распространения волны - это источник отражений. Неоднородности всегда локализованы в простран­стве в том смысле, что есть возможность указать их координату в любой момент времени. Поэтому численное значение коэффициента отраже­ния, как величины, которую необходимо измерить, всегда указывают для определенной координаты в пространстве. Само понятие “неоднородность” предполагает, что какое-то свойство среды, в которой распространяется волна, изменяется. В инженерной практике измеряются неоднородности относительно трех стандартизо­ванных сред распространения электромагнитных волн:

- свободного пространства;

- волноводов прямоугольного сечения;

- коаксиальных трактов.

Например, в свободном пространстве - в атмосфере Земли - неоднородностями являются ионосферный слой, тучи, различные летающие объекты - радиолокационные цели, а также сооружения, здания и т. п. предметы. Простейший пример такой неоднородности - это гладкая поверхность Земли - почва, вода в водоеме в виде плоскости раздела двух сред с различными значениями диэлектрической и магнит­ной проводимости ε, m и активными потерями, характеризуемыми значением .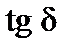

В закрытых неизлучающих передающих линиях можно говорить о неоднородности в волноводе (полом прямоугольном или круглом, коак­сиальном, полосковой линии симметричной или несимметричной) опре­деленного поперечного сечения, в котором распространяется вполне определенный тип электромагнитной волны. Простейшие примеры неоднородности волноводного тракта - изгибы вдоль оси распространения волн, изменение размеров попереч­ного сечения, изменения ε, m, 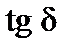заполнения - различные диэлектри­ческие пробки, отверстия в стенках и тому подобные нарушения одно­родности. Важно понять, что в определенной плоскости расположения неоднородности возникают отражения, которые характеризуются численными значениями безразмерной величины - коэффициента отражения, которую необходимо измерять.