Случайные погрешности измерений. Свойства случайных погрешностей.

Случайная погрешность - это составляющая погрешности результата измерений, изменяющаяся случайным образом (по знаку и значению) в серии повторных измерений, проведенных с одинаковой тщательностью, одного и того же размера ФВ. Отметим следующие существенные стороны данного определения.

1) Случайные погрешности неизбежны и неустранимы и всегда присутствуют в результатах измерений. Они вызывают рассеяние результатов при многократном и достаточно точном измерении одной и той же величины, вызывая различие результатов в последних значащих цифрах результата.

2) Случайные погрешности - это погрешности, в появлении которых нет какой-либо закономерности, кроме той закономерности, что предсказать конкретное значение их в конкретном результате невозможно. Численные значения случайных погрешностей являются случайными числами.

3) Выявить наличие случайных погрешностей и их значения можно только выполняя повторные измерения, то есть, производя ряд измерений. Однако, априорное утверждение об их наличии бесспорно верное.

Имеется несколько способов выражения случайной погрешности.

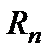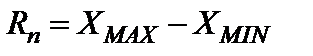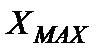Размах результатов измерений - одна из наиболее простых оценок рассеяния результатов единичных измерений ФВ, образующих ряд (или выборку из n измерений), вычисляемая по формуле , где и 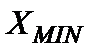- наибольшее и наименьшее значения ФВ в данном ряду измерений. В некоторых случаях, особенно при малых 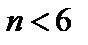( 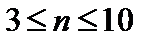), размах является приемлемой оценкой рассеяния результатов измерений, ибо имеет связь со средней квадратической погрешностью единичного измерения (в ряду равноточных измерений).

Средняя квадратическая погрешность (СКП) единичного измерения (однократного измерения в ряду равноточных многократных измерений) - обобщенная характеристика рассеяния результатов, полученных в ряду независимых равноточных измерений одной и той же ФВ. вследствие влияния случайных погрешностей, вычисляемая по формуле:

(2.5)

где S - средняя квадратическая погрешность единичного результата измерений, входящего в ряд из n измерений;

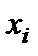- результат отдельного измерения в ряду измерений;

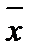- среднее арифметическое из результатов n измерений.

Средняя арифметическая погрешность единичного измерения (в ряду измерений) - это обобщенная характеристика рассеяния отдельных результатов равноточных независимых измерений, входящих в ряд из n измерений, вычисляемая по формуле:

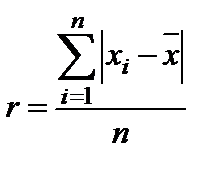(2.11)

где r - средняя арифметическая погрешность;

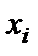- результат i-го измерения, входящего в ряд измерений;

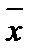- среднее арифметическое из n значений величины;

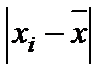- абсолютное значение погрешности i-го измерения.