Задачи для самостоятельного решения. 1. Два проводящих шара с радиусом 5 см каждый заряжены до потенциалов 60 и 150 В
1. Два проводящих шара с радиусом 5 см каждый заряжены до потенциалов 60 и 150 В. Определить потенциал шаров и изменение заряда каждого шара после их соприкосновения в случае одноименно и разноименно заряженных шаров.
Ответ: После соприкосновения одноименно заряженных шаров их потенциал равен 100 кВ, изменение потенциала 30 нКл. Для разноименно заряженных шаров: -50 кВ и 60 нКл.
2. Маленький шарик массой m висит на тонкой нити между двумя параллельными вертикальными струнами, находящимися на расстоянии d друг от друга. При какой разности потенциалов между пластинами угол отклонения от вертикали станет равным a, если заряд шарика q?
Ответ: 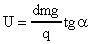
ПОСТОЯННЫЙ ТОК
| определения | законы |
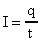 - сила электрического тока, А - сила электрического тока, А
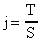 - плотность тока, - плотность тока, 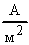
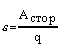 - электродвижущая сила источника тока, В - электродвижущая сила источника тока, В
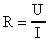 - электрическое сопротивление, Ом - электрическое сопротивление, Ом
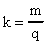 - электрический эквивалент, кг/Кл - электрический эквивалент, кг/Кл
| 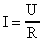 - закон Ома для однородного участка цепи - закон Ома для однородного участка цепи
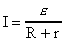 - закон Ома для полной цепи - закон Ома для полной цепи
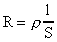 - зависимость сопротивления от длины и сечения проводника - зависимость сопротивления от длины и сечения проводника
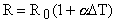 - зависимость сопротивления от температуры - зависимость сопротивления от температуры
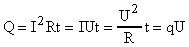 - закон Джоуля-Ленца - закон Джоуля-Ленца
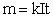 - закон электролиза - закон электролиза
|
Примеры решения задач
Пример 1. Участок цепи состоит из двух источников тока, соединенных в батарею одноименными полюсами. e1 = 12 B, r1 = 0,1 Ом, e2 = 6 B, r2 = 0,2 Ом.
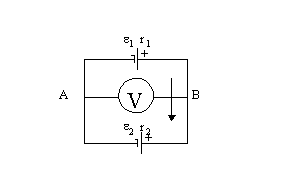
Найти показание вольтметра, подключенного к полюсам источника тока.
Решение.
Для упрощения задачи считаем сопротивление соединительных проводов бесконечно малым, а сопротивление вольтметра бесконечно большим.
Вольтметр измеряет разность потенциалов между точками А и В данной цепи, то есть на концах участка Аe1B (или участки Аe2B).
1. Сначала рассчитаем силу тока в контуре. Она одинакова как для выходного участка, так и для нижнего участка данной цепи, поскольку ток через вольтметр практически не идет. В нашем случае имеем неразветвленную цепь, можно воспользоваться законом Ома для полной цепи: 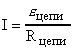 , где
, где 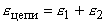 - алгебраическая сумма ЭДС отдельных источников,
- алгебраическая сумма ЭДС отдельных источников, 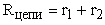 - полное сопротивление цепи.
- полное сопротивление цепи.
Знаки ЕДС определяются после выбора положительного направления обхода контура. Если обходить контур по часовой стрелке, как показано на рисунке, то e1>0, e2 < 0 (при переходе от "-" к "+" ЭДС считается положительной). Таким образом, в нашем случае
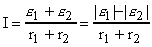 ;
; 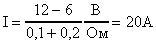 .
.
В случае разветвленной цепи с одним источником также "работает" закон Ома, лишь только сопротивление цепи надо рассчитывать сначала для участков с параллельным соединением, затем общее сопротивление последовательно соединенных участков.
В общем случае разветвленной цепи следует применять правила Кирхгофа.
Правило Кирхгофа для контура: 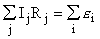 , - алгебраическая сумма произведений силы тока на сопротивление, подсчитанная для участков замкнутого контура, равна алгебраической сумме ЭДС, действующих в данном контуре (ток, совпадающий с направлением обхода контура определяется, как показано ранее).
, - алгебраическая сумма произведений силы тока на сопротивление, подсчитанная для участков замкнутого контура, равна алгебраической сумме ЭДС, действующих в данном контуре (ток, совпадающий с направлением обхода контура определяется, как показано ранее).
Правило Кирхгофа для узла: 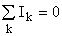 , - алгебраическая сумма токов, сходящихся в точке разветвления проводников, равна нулю. (токи, входящие в узел, принято считать положительными, выходящие - отрицательными). Это правило следует из условия постоянства тока. В цепи постоянного тока потенциалы точек цепи постоянны во времени, заряды в узлах не накапливаются.
, - алгебраическая сумма токов, сходящихся в точке разветвления проводников, равна нулю. (токи, входящие в узел, принято считать положительными, выходящие - отрицательными). Это правило следует из условия постоянства тока. В цепи постоянного тока потенциалы точек цепи постоянны во времени, заряды в узлах не накапливаются.
Легко видеть, что правило Кирхгофа для контура является обобщением закона Ома для полной цепи.
В нашей задаче согласно этому правилу получим, полагая что ток идет по направлению обхода контура (по часовой стрелке).
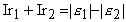 ,
,
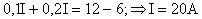 .
.
2. Разность потенциалов на участке АВ, измеряемая вольтметром, может быть рассчитана как для верхнего (с ЭДС e1), так и для нижнего участка (с ЭДС e2).
На участке А1e1В происходит падение потенциала Ir1 вдоль на сопротивлении r1 и повышения потенциала на полюсах источника, равное по модулю e1.
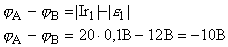
Знак "-" означает, что jB > jA.
Для участка А1e2В разность потенциалов как падение потенциала Ir2 вдоль участка с сопротивлением r2 и понижение потенциала на полюсах источника тока, так как переход от B к А вдоль тока через источник происходит от "+" к "-"
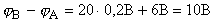 .
.
Как и следовало ожидать, получено тоже число, но с положительным знаком, что тоже не удивительно, так как jB > jA уже известно.
Вообще, для любого участка цепи можно записать 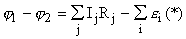 .
.
Если направление обхода выбирается от 1 к 2 вдоль направления тока, то все слагаемые 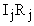 положительны, а знак ЭДС
положительны, а знак ЭДС 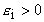 при переходе от "-" к "+" источника ei < 0 в противном случае.
при переходе от "-" к "+" источника ei < 0 в противном случае.
В нашей задаче формальное следование закону Ома для неоднородного участка цепи (*) приводит к уравнению: 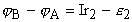 . Знак ЭДС, получим
. Знак ЭДС, получим 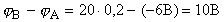 .
.
Ответ: Вольтметр показывает разность потенциалов 10 В.
Пример 2. Линия из медного провода сечением 25 мм2 и длиной 100 м соединяет генератор с электродвигателем. Сила тока в цепи 40 А при напряжении на клеммах электродвигателя 220 В. Найдите мощность электрического тока, потребляемую двигателем, мощность потерь в линии, напряжение на клеммах генератора. Учтите, что линия двухпроводная.
Рдв = ? Рл = ? Uг = ?
S = 2510-4 м2; l = 2100 м; I = 40 А; Uдв = 220 В; r = 1.710-8 Омм.
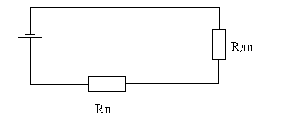
Электрическая энергия, вырабатываемая генератором, преобразуется в джоулево тепло 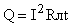 ( потери в линии) и в механическую энергию (в электродвигателе).
( потери в линии) и в механическую энергию (в электродвигателе).
Таким образом, согласно закону сохранения и превращения энергии 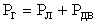 , где
, где 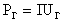 - мощность генератора,
- мощность генератора, 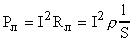 - мощность потерь в линии;
- мощность потерь в линии; 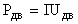 - мощность, потребляемая электродвигателем.
- мощность, потребляемая электродвигателем.
Учитывая, что сила тока во всех участках при последовательном соединении одинакова, получим: 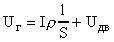 или
или  , где Uг - потери напряжения в линии.
, где Uг - потери напряжения в линии.
Отсюда, Uг = 40 А1,710-8 Омм 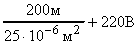 = 5,4 В + 220 В = 225,4 В.
= 5,4 В + 220 В = 225,4 В.
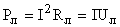 ; Pл =40А5,4В=0,22103 Вт
; Pл =40А5,4В=0,22103 Вт
Рдв = 40А220В = 8,8103 Вт.
Ответы: мощность электродвигателя 8,8 кВт, мощность потерь в линии 0,22 кВт, напряжение на клеммах генератора 225,4 В.
Пример 3. Для электролиза меди включено последовательно 400 гальванических ванн с площадью катодных пластин 16 м2 каждая. Плотность тока 200 А/м2. Найти выпуск меди за сутки и расход электроэнергии за это же время, если общее напряжение на ваннах равно 1000 В.
m = ?; Aэл = ?
S = 16 м2, N = 400; j = 200 А/м2; t = 243600 с; U = 100 В; k = 0,3310-6 кг/Кл
Решение:
По закону Фарадея для электролиза 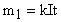 найдем массу меди, выделившейся на катодной пластинке в одной ванне. Так как ванны соединены последовательно, сила тока в ваннах одинакова. Следовательно, масса меди во всех ваннах
найдем массу меди, выделившейся на катодной пластинке в одной ванне. Так как ванны соединены последовательно, сила тока в ваннах одинакова. Следовательно, масса меди во всех ваннах 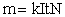 , где сила тока I = jS. Отсюда
, где сила тока I = jS. Отсюда 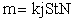 .
.
Проверим размерность единиц массы:
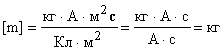 ;
;
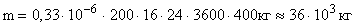 .
.
Расход электроэнергии равен работе тока за время электролиза
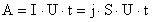 ;
;
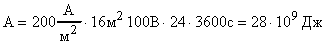 .
.
Ответ: масса меди, выделившейся на катодных пластинах во всех ваннах за сутки, равна 36 m, расход энергии 28 ГДж.
Дата добавления: 2017-02-04; просмотров: 642;
