Уравнения переходных процессов в цепях с распределенными параметрами
При рассмотрении схемы замещения цепи с распределенными параметрами были получены дифференциальные уравнения в частных производных
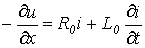 ; ;
| (5) |
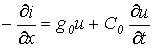
| (6) |
Их интегрирование с учетом потерь представляет собой достаточно сложную задачу. В этой связи будем считать цепь линией без потерь, т.е. положим 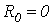 и
и 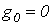 . Такое допущение возможно для линий с малыми потерями, а также при анализе начальных стадий переходных процессов, часто наиболее значимых в отношении перенапряжений и сверхтоков.
. Такое допущение возможно для линий с малыми потерями, а также при анализе начальных стадий переходных процессов, часто наиболее значимых в отношении перенапряжений и сверхтоков.
С учетом указанного от соотношений (5) и (6) переходим к уравнениям
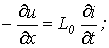
| (7) |
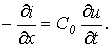
| (8) |
Для получения уравнения (7) относительно одной переменной продифференцируем (7) по х, а (8) – по t:
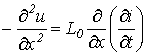 ; ;
| (9) |
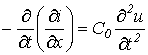 . .
| (10) |
Учитывая, что для линии без потерь 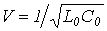 , после подстановки соотношения (10) в (9) получим
, после подстановки соотношения (10) в (9) получим
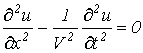 . .
| (11) |
Аналогично получается уравнение для тока
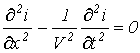 . .
| (12) |
Волновым уравнениям (11) и (12) удовлетворяют решения
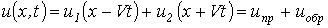 ;
;
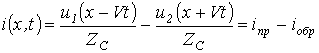 .
.
Как и ранее, прямые и обратные волны напряжения и тока связаны между собой законом Ома для волн
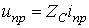 и
и 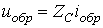 ,
,
где 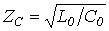 .
.
При расчете переходных процессов следует помнить:
- В любой момент времени напряжение и ток в любой точке линии рассматриваются как результат наложения прямой и обратной волн этих переменных на соответствующие величины предшествующего режима.
- Всякое изменение режима работы цепи с распределенными параметрами обусловливает появление новых волн, накладываемых на существующий режим.
- Для каждой волны в отдельности выполняется закон Ома для волн.
Как указывалось, переходный процесс в цепях с распределенными параметрами характеризуется наложением многократно отраженных волн. Рассмотрим многократные отражения для двух наиболее характерных случаев: подключение источника постоянного напряжения к разомкнутой и короткозамкнутой линии.
Дата добавления: 2017-02-04; просмотров: 482;
