Уравнения длинной линии как четырехполюсника
В соответствии с (11) и (12) напряжения и токи в начале и в конце линии связаны между собой соотношениями
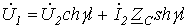 ;
;
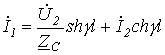 .
.
Эти уравнения соответствуют уравнениям симметричного четырехполюсника, коэффициенты которого 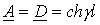 ;
; 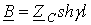 и
и 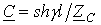 ; при этом условие
; при этом условие 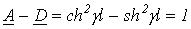 выполняется.
выполняется.
Указанное означает, что к длинным линиям могут быть применены элементы теории четырехполюсников, и, следовательно, как всякий симметричный четырехполюсник, длинная линия может быть представлена симметричной Т- или П- образной схемами замещения.
Определение параметров длинной линии из опытов холостого хода и короткого замыкания
Как и у четырехполюсников, параметры длинной линии могут быть определены из опытов холостого хода (ХХ) и короткого замыкания (КЗ).
При ХХ 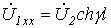 и
и 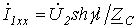 , откуда входное сопротивление
, откуда входное сопротивление
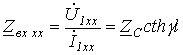 . .
| (13) |
При КЗ 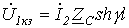 и
и 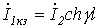 . Следовательно,
. Следовательно,
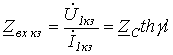 . .
| (14) |
На основании (13) и (14)
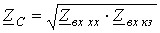
| (15) |
и
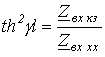 ,
,
откуда
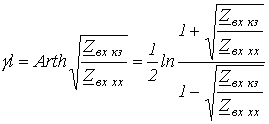 . .
| (16) |
Выражения (15) и (16) на основании данных эксперимента позволяют определить вторичные параметры 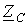 и
и 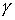 линии, по которым затем могут быть рассчитаны ее первичные параметры
линии, по которым затем могут быть рассчитаны ее первичные параметры 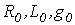 и
и 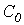 .
.
Линия без потерь
Линией без потерь называется линия, у которой первичные параметры  и
и 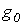 равны нулю. В этом случае, как было показано ранее,
равны нулю. В этом случае, как было показано ранее, 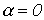 и
и 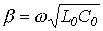 . Таким образом,
. Таким образом,
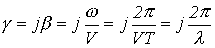 ,
,
откуда 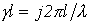 .
.
Раскроем гиперболические функции от комплексного аргумента 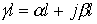 :
:
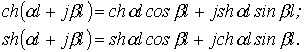
Тогда для линии без потерь, т.е. при 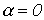 , имеют место соотношения:
, имеют место соотношения:
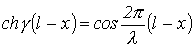 и
и 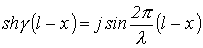 .
.
Таким образом, уравнения длинной линии в гиперболических функциях от комплексного аргумента для линии без потерь трансформируются в уравнения, записанные с использованием круговых тригонометрических функций от вещественного аргумента:
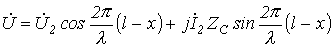 ; ;
| (17) |
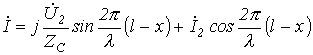 . .
| (18) |
Строго говоря, линия без потерь (цепь с распределенными параметрами без потерь) представляет собой идеализированный случай. Однако при выполнении 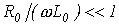 и
и 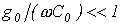 , что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
, что имеет место, например, для высокочастотных цепей, линию можно считать линией без потерь и, следовательно, описывать ее уравнениями (17) и (18).
Дата добавления: 2017-02-04; просмотров: 499;
