Действия над случайными величинами
1. Сумма (разность) случайных величин. Пусть Х, Y – случайные величины с функциями распределения Fx(x) и Fy(y) соответственно. Суммой Z = X ± Y называется с.в. Z с функцией распределения Fz(z)=P(X±Y<z).
2. Произведением с.л. Х, Y называется с.в. Z= X Y с функцией распределения Fz(z)=P(XY<z).
3. Произведением числа С на с.в. Х называется с.в. Z = СХ с функцией распределения Fz(z) = P(СХ<z).
4.2 Независимые случайные величины. Пусть Х, Y – случайные величины с функциями распределения Fx(x) и Fy(y) соответственно. Функцией совместного распределения двух с.в. Х, Y называется функция от двух переменных
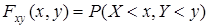 .
.
Здесь под {X<x, Y<y} понимается произведение событий {X<x} и {Y<y}.
Плотностью совместного распределения непрерывных с.в. Х, Y называется функция
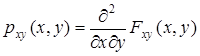 .
.
С.в Х, Y называются независимыми, если 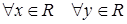
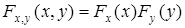 . (4.1)
. (4.1)
Из этого равенства следует, что 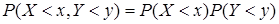 . По определению условной вероятности
. По определению условной вероятности
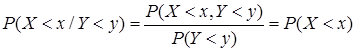 .
.
Смысл этого равенства состоит в том, что независимость с.в. Х, Y означает, что закон распределения одной из них не изменяется от того, какое значение приняла другая в результате проведения опыта.
Если с.в. Х, Y – НСВ с плотностями 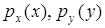 соответственно, то их независимость означает
соответственно, то их независимость означает
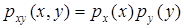
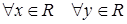 (4.2)
(4.2)
Для ДСВ Х, Y их независимость означает
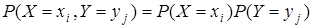
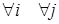 (4.3)
(4.3)
4.3 Свойства математического ожидания
Доказательства свойств проведем для ДСВ.
1. M[C]=C, где С=const. Действительно, P(X=C)=1. M[C]=C P(X=C)=C.
2. M[CX]=C×M[X], С – константа.
Закон распределения с.в. СХ имеет вид: С xi ® рi . Тогда
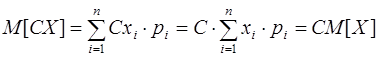 .
.
3. M[X+Y]=M[X]+M[Y]. В частности, M[X+a]=M[X]+a, a=const.
Обозначим 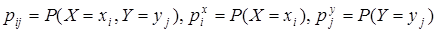 .Тогда
.Тогда
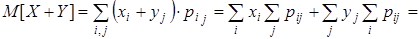
= 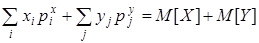
В предпоследнем равенстве воспользовались свойством 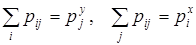 .
.
4. M[X]×M[Y] = M[X]×M[Y], если с.в. X,Y независимы.
Поскольку X,Y независимы, то из (4.3) следует 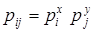 . Тогда
. Тогда
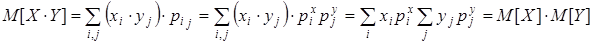 .
.
5. Пусть с.в. Y является функцией j(X) от с.в. X. Тогда для верны формулы
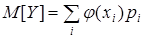 для ДСВ,
для ДСВ,
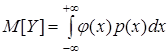 для НСВ.
для НСВ.
Действительно, закон распределения с.в. Y имеет вид 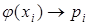 . Все равные значения
. Все равные значения 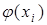 заменяются одним, а соответствующие вероятности складываются. Тогда по определению м.о.
заменяются одним, а соответствующие вероятности складываются. Тогда по определению м.о. 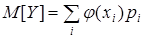 .
.
Пример. 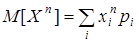 для ДСВ и
для ДСВ и 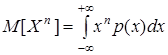 для НСВ.
для НСВ.
Свойства дисперсии
1. 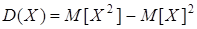 .
.
2. 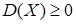 .
.
3 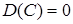 , C=const.
, C=const.
4. 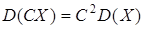 , C=const.
, C=const.
5. D(X+Y)=D (X)+D(Y), если с.в. X,Y независимы.
В частности, D(X+C)=D(X), C=const;
Докажем равенство 1.
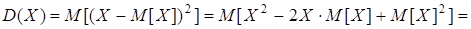
= 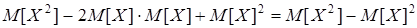 .
.
Использованы свойства м.о. и тот факт, что M [X] = const.
Доказательство 5. По свойству 1 имеем D(X+Y)=M[(X+Y)2]–(M[X]+ M[Y])2=
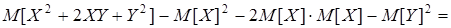
= 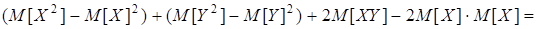
По свойству 4 м.о. 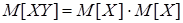 .
.
= 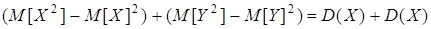 .
.
Дата добавления: 2017-02-04; просмотров: 1724;
