Другие числовые характеристики

Начальным моментом k-го порядка случайной величины X называется математическое ожидание случайной величины X^k

.

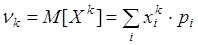Заметим n₁=M[X].

Центральным моментом k-го порядка называется .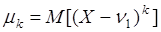

Заметим, что .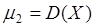

Медиана – это такое число Ме(Х), что F(Ме(Х))=0,5.

Мода – точка максимума плотности распределения. Если у с.в. одна мода, то распределение называется унимодальным.

Квантилью порядка a (0<a<1) называется такое число x_a, что F(x_a)= a. Заметим, что квантиль порядка 0,5 совпадает с медианой.

Коэффициентом асимметрии называется число .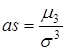

Коэффициентом эксцесса называется число .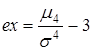

4.6 Нормальное распределение (распределение Гаусса)

Случайная величина Х называется нормально распределенной (имеющей распределение Гаусса), если ее плотность вероятности имеет вид

.

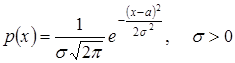Нормальное распределение будем обозначать N(a,s). Тогда XÎN(a,s) означает, что с.в. X имеет нормальное распределение с параметрами a,s. Плотность зависит от двух параметров a и s > 0, смысл которых выясним в дальнейшем.

Функция распределения равна

.

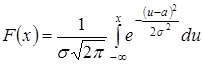Докажем, что плотность распределения удовлетворяет свойству 4 нормировки плотности распределения (лекция 3).

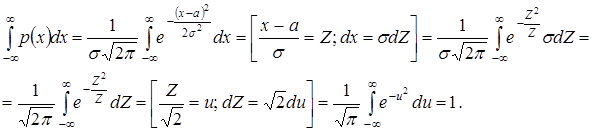
График плотности нормального распределения см. на рисунке 4.1.

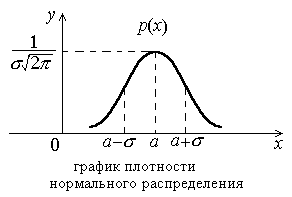Рисунок 4.1

Если параметры a = 0, σ = 1, то такая нормально распределенная случайная величина называется стандартной нормальной случайной величиной.

В природе часто встречаются нормально распределенные с.в. Так, «естест-венные» размеры человека (рост, вес и т.д.), деревьев (высота, диаметр ствола) распределены нормально. Причина этого явления раскрывается в теореме Ляпунова, о которой речь пойдет в дальнейшем.