Векторная нетопологическая модель

Векторно-нетопологическое представление данных (модель) - цифровое представление точечных, линейных и полигональных пространственных объектов в виде набора координатных пар, с описанием только геометрии объектов.

Пространственная информация о географических объектах представляется наборами элементарных графических примитивов – точек, линий, областей (полигонов).

Семантическая информация, передается условными знаками (символами и цветом) и надписями (например, название улицы, этажность дома).

Векторные модели строятся на векторах, занимающих часть пространства в отличие от занимающих все пространство растровых моделей. Это определяет их основное преимущество - меньший объем памяти для хранения и меньшие затраты времени на обработку и представление, более высокая точность позиционирования и представления данных.

При построении векторных моделей объекты создаются путем соединения точек прямыми линиями, дугами окружностей, полилиниями. Площадные объекты - задаются наборами линий.

Каждое векторное образование в цифровой форме представляется координатными парами X,Y.

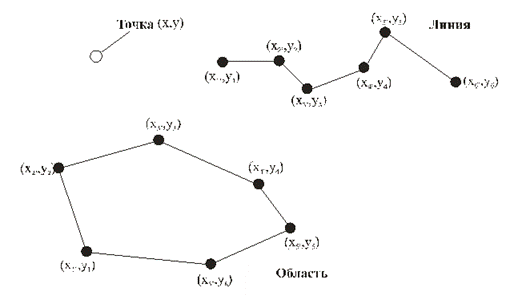
Рис.6. Векторное представление пространственных объектов

Точечный географический объект представляется одной координатной парой X,Y.

Линейный географический объект представляется последовательностью координатных пар X1,Y1;X2,Y2; X3,Y3;…сегментов полилинии.

Полигональный географический объект представляется последовательностью координатных пар X1,Y1; X2,Y2; X3,Y3;…; X1,Y1. сегментов полигона. В этом списке совпадение первой и последней пары координат означает, что полигон замкнутый.

При описании множества полигонов, каждый отрезок границы, заключенный между двумя узловыми точками (за исключением внешней границы полигонов), будет описан в этом случае дважды (по и против часовой стрелки).

Такая модель данных для описания точечных, линейных и полигональных объектов носит наименование модели «спагетти» и поддерживается недорогими программными средствами настольного картографирования и ГИС.

Так как спагетти-модель очень сильно напоминает бумажную карту, она является эффективным методом картографического отображения и часто используется в компьютеризованной картографии, где анализ не является главной целью.

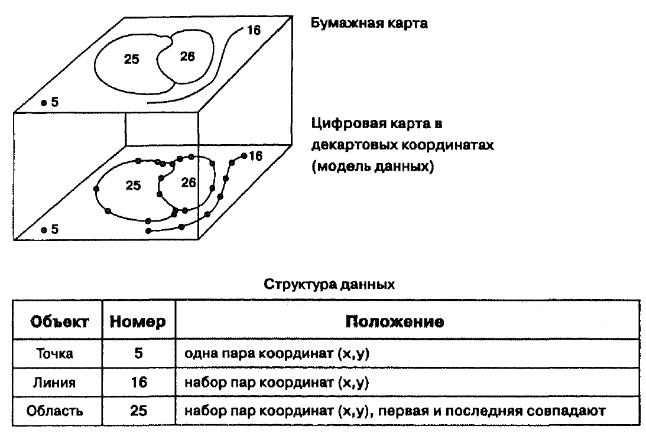
Рис. 7. Векторная модель «спагетти».

8.3.2. Векторная топологическая модель

Векторно-топологическое представление (линейно-узловое представление) - разновидность векторного представления линейных и полигональных пространственных объектов, описывающего не только их геометрию, но и топологические отношения между полигонами, дугами и узлами.

Векторную топологическую модель называют линейно-узловой моделью. Главные ее элементы (примитивы):

- промежуточная точка;

- сегмент (линейный сегмент, отрезок прямой);

- узел;

- дуга;

- полигон (область, полигональный объект, многоугольник, контур, контурный объект).

Топологические модели, содержат топологическую информацию в явном виде, которая описывается набором узлов и дуг.

Узел- обычно это пересечение двух или более дуг, и его номер используется для ссылки на любую дугу, которой он принадлежит.

Каждая дуганачинается и заканчивается либо в точке пересечения с другой дугой, либо в узле, не принадлежащем другим дугам.

Дуги образуются последовательностями отрезков, соединенных промежуточными точками. В этом случае каждая линия имеет два набора чисел: пары координат промежуточных точек и номера узлов. Кроме того, каждая дуга имеет свой идентификационный номер, который используется для указания того, какие узлы представляет ее начало и конец.

Области, ограниченные дугами, также имеют идентифицирующие их коды, которые используются для определения их отношений с дугами. Далее, каждая дуга содержит явную информацию о номерах областей слева и справа от нее, что позволяет находить смежные области. Эта особенность данной модели позволяет компьютеру знать действительные отношения между графическими объектами.

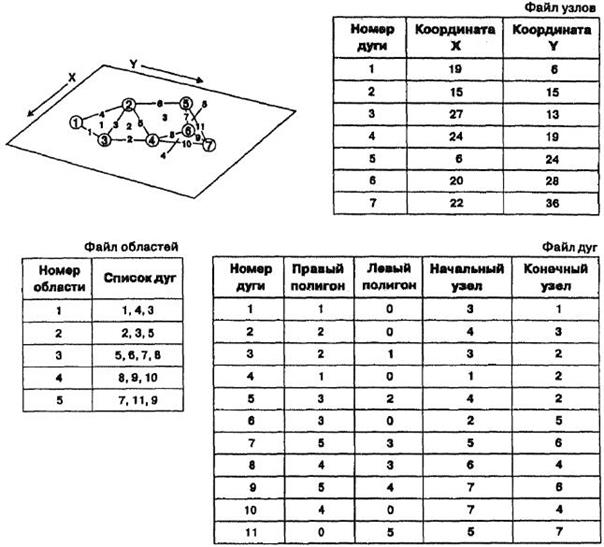
Рис. 8. Векторная топологическая модель