Тонкостенные сосуды

Оболочки, имеющие форму тел вращения (рис. 11.1), стенки которых тонки (t ≤ 0,1D₀), не имеют резких переходов и изломов при действии осесимметричных нагрузок (например, давления жидкости или газа), попадают под класс тонкостенных сосудов и могут быть рассчитаны по безмоментной теории.

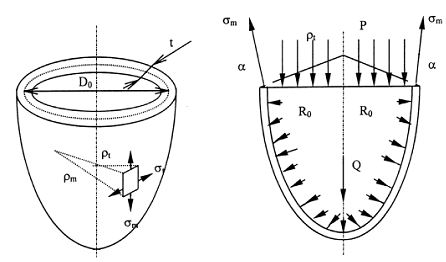
Рис. 11.1

Связь между меридиональными σ_m и кольцевыми σ_t нормальными напряжениями (рис. 11.1) описывается уравнением Лапласа:

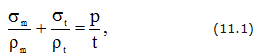
где ρ_m и ρ_t – радиусы кривизны серединной поверхности меридионального и кольцевого сечений на уровне рассматриваемой точки;

р – интенсивность внутреннего давления.

Для определения σ_m обычно используется зависимость

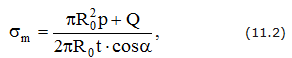
где Q – вес части сосуда и жидкости ниже рассматриваемого сечения.

Уравнения (11.1) и (11.2) позволяют найти величины σ_m и σ_t в каждой точке сосуда.

Рассмотрим частные случаи:

Сферический сосуд под действием внутреннего давления газа (рис.11.2).

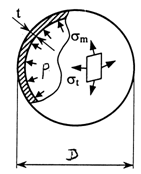
Рис. 11.2

Благодаря симметричности сосуда σ_m = σ_t = σ, ρ_m = ρ_t = D/2.

Из уравнения (11.1) находим

Цилиндрический сосуд под действием внутреннего давления газа (рис. 11.3).

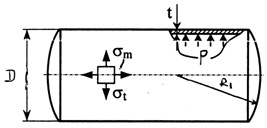
Рис. 11.3

Для цилиндрической части сосуда имеем:

ρ_t = D/2; ρ_m = ∞; α=0

Из уравнения (11.1) находим σ_t = pD/2t. (11.4)

Из уравнения (11.2), полагая cos α = 1, Q = 0, σ_m = pD/4t. (11.5)

Напряжения в днищах определяем, как в сферическом сосуде:

σ_m(дн)= σ_t(дн)=pR₁/2t. (11.6)

Напряжения в стенке трубы определяются аналогично, как для цилиндрической части тонкостенного сосуда.

Сравнение (11.4) и (11.5) показывает, что σ_t =2σ_m , т.е. напряжения, растягивающие стенки цилиндрической части сосуда, по окружности в 2 раза больше напряжений вдоль образующей. Поэтому разрушение котлов, труб обычно происходит от кольцевых напряжений вдоль образующей.

σ_m и σ_t являются главными напряжениями, σ_t = σ₁ , σ_m = σ₂ . Третье главное напряжение, перпендикулярное к поверхности сосуда

со стороны, где действует давление, σ₃ = -р ;

с противоположной стороны, σ₃ =0.

В тонкостенных оболочках обычно величины σ_m и σ_t намного больше, чем интенсивность внутреннего давления р, и поэтому величиной σ₃ можно пренебречь, т.е. считать равной нулю.

Так как в любой точке тонкостенного сосуда имеет место сложное напряженное состояние, для расчета на прочность в зависимости от материала следует пользоваться соответствующей гипотезой прочности

σ_эквI ≤ [σ]_p

Для рассматриваемой задачи при неучете σ₃ эквивалентные напряжения по третьей гипотезе прочности и по гипотезе Мора одинаковы, т.е.

σ_экв^III= σ_эквМ= σ_t (11.7)

а по энергетической теории

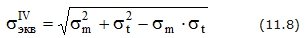
Если тонкостенный сосуд имеет резкие переломы в очертании (например, примыкание днищ к цилиндрической части), а также в местах закрепления, приложения сосредоточенных сил, установки патрубков, фланцев, у краев оболочки возникает изгиб. Зоны, прилегающие к таким местам, должны рассчитываться по моментной теории.