Центральное (осевое) растяжение-сжатие

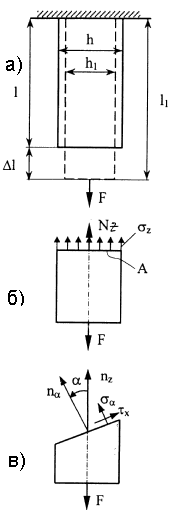
Осевым растяжением (сжатием) брусьев называют такой вид деформирования, при котором в их поперечных сечениях возникает единственный внутренний силовой фактор – продольная сила N_z.

Для определения продольной силы используется метод сечений (Рис. 4.1,б).

N_z= Σ F_z^вн (4.1)

Напряжения

N_z равномерно распределяется по площади поперечного сечения, вызывая нормальные напряжения.

В наклонном сечении возникают нормальные σ_α и касательные τ_α напряжения (рис. 4.1,в).

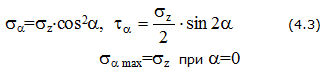
причем

Деформации

При растяжении (сжатии) наблюдаются абсолютные и относительные деформации (рис. 4.1,а):

l₁ – l = Δl - абсолютная продольная деформация (удлинение);

h₁ – h = -Δh - абсолютная поперечная деформация (сужение);

относительная продольная деформация:

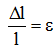
относительная поперечная деформация:

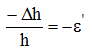
Отношение

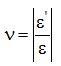
называется коэффициентом поперечной деформации (коэффициентом Пуассона).

Напряжения и деформации взаимосвязаны законом Гука

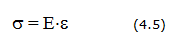
где Е - модуль упругости (модуль Юнга).

В общем случае удлинение стержня определяется по формуле

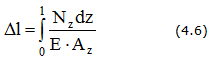
В частном случае, когда жесткость сечения ЕА = const и N_Z = F = const

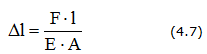
При ступенчатом изменении нагрузки N_z и конфигурации сечения

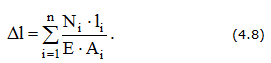
В результате деформации бруса его поперечные сечения получают линейные перемещения U_(z). Так, перемещение сечения В, находящегося на расстоянии z от закрепленного конца, равно удлинению Δl_z части бруса длиной z, заключенной между неподвижным и рассматриваемым сечением.

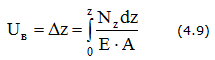Взаимное перемещение двух сечений В и С бруса равно удлинению части бруса, заключенной между этими сечениями

U_(B-C)= Δl_B-C (рис.4.2)

Рис. 4.2

Перемещение точек стержневой системы (BCD) (Рис. 4.3) происходит как за счет продольных деформаций (U_СВ = Δl_BC , U_CD = Δl_DC ), так и за счет поворота деформированных стержней BC₁ и DC₂ относительно шарниров (B, D) как твердого тела по дугам С₁С₃ = δ₁ и С₂С₃ = δ₂, замененными перпендикулярами к радиусам поворота (ВС₁ и DС₂). Отрезок СС₃ = δ_с соответствует полному перемещению узла С в результате деформации стержней ВС и DС.

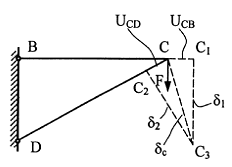
Рис. 4.3