Внецентренное продольное нагружение

Внецентренным нагружением называют случай, когда продольная сжимающая либо растягивающая сила приложена не в центре тяжести сечения, а с некоторым смещением от нее, называемым эксцентриситетом (рис. 7.2).

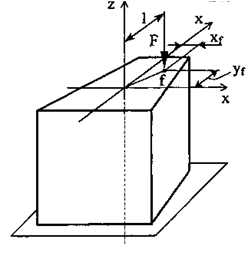
Рис. 7.2

Распределение напряжений (рис. 7.3):

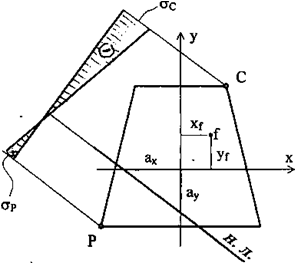
Рис. 7.3

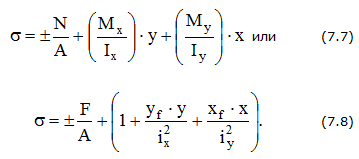
Знак “+” соответствует растяжению, а знак ” - ” – сжатию.

Отрезки, отсекаемые нейтральной линией на осях координат

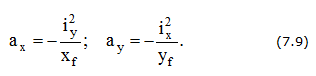
Условие прочности

Условия прочности при внецентренном сжатии

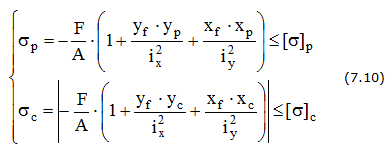
Ядро сечения

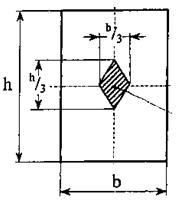
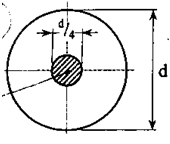
Рис. 7.4

Координаты вершин ядра сечения (рис. 7.4):

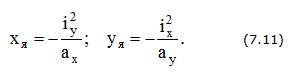
Сложное сопротивление

Изгиб с кручением

Данный вид деформации имеет место когда в сечениях бруса одновременно возникают изгибающий и скручивающий моменты (рис. 7.5)

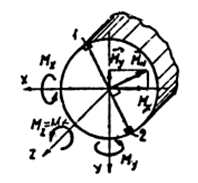
Рис. 7.5

Условие прочности

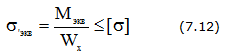
Эквивалентный момент М_экв рассчитывается по одной из гипотез прочности:

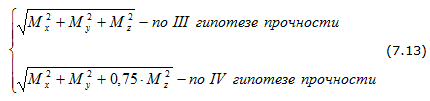
Устойчивость элементов конструкций

Продольный изгиб

Формула Эйлера (стержни большой гибкости, для которых σ_кр < σ_пц)

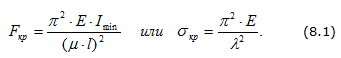
Формула Тетмайера - Ясинского (стержни средней гибкости σ_кр > σ_пц)

- для пластичных материалов

F_кp = А ⋅ (а - b⋅ λ) (8.2)

- для хрупких материалов

F_кp = А ⋅ (а - b⋅X + с ⋅ λ² ), (8.3)

где а, b, с - коэффициенты, полученные экспериментально для различных материалов.

Гибкость стержня

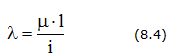
Коэффициент приведения длины μ (рис. 8.1)

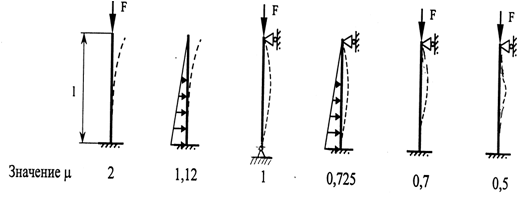
Рис. 8.1

Условие устойчивости σ= F/(φ⋅A)≤ [σ], (8.5)

где φ - коэффициент продольного изгиба

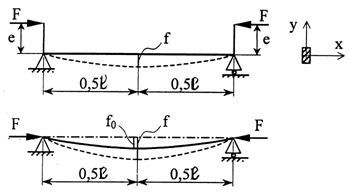
Рис. 8.2

Внецентренное приложение нагрузки (рис 8.2,а)

F = 4e/π ⋅ F/F_э ⋅ 1/(1 – F/F_э) (8.6)

F_э = π²⋅Е⋅I_x/(μ⋅l)² - Эйлерова сила (8.7)

Стержень с начальным искривлением (рис 8.2,б)

f = f₀ ⋅ F/(1 – F/F_э) (8.8)