Расчеты на прочность при напряжениях, циклически изменяющихся во времени

В подавляющем большинстве случаев напряжение изменяется периодически (рис. 10.1). Совокупность всех значений напряжений в течении одного периода называется циклом напряжений.

Характеристиками циклов напряжений являются:

1) максимальное напряжение цикла – σ_max;

2) минимальное напряжение цикла – σ_min;

3) среднее напряжение цикла – σ_m=( σ_max + σ_min)/2;

4) амплитуда цикла – σ_a = ( σ_max – σ_min)/2;

5) Коэффициент асимметрии цикла – r = σ_min / σ_max .

Циклы, имеющие одинаковые коэффициенты асимметрии цикла, называются подобными.

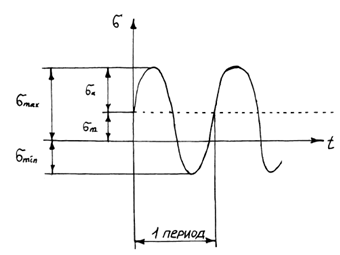
Рис. 10.1

Наиболее распространенными являются:

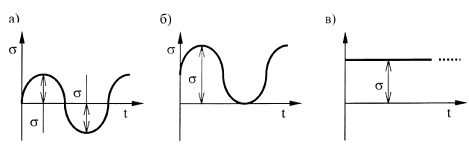
Рис. 10.2

1) Симметричный цикл (рис. 10.2,а), в котором σ_a= σ_max = - σ_min. При этом σ_m=0, r=-1.

2) Отнулевой (пульсирующий) цикл (рис. 10.2,б). Для этого случая

σ_max= σ, σ_min=0, σ_m= σ_a= σ/2, r=0.

3) Статическое напряжение иногда называют постоянным циклом (рис. 10.2,в), в нем

σ_a=0, σ_max = σ_min= σ_m= σ, r=+1.

Любой асимметричный цикл можно представить как сумму симметричного цикла и постоянного напряжения.

В случае действительных переменных касательных напряжений остаются в силе все термины и соотношения, с заменой σ на τ .

Для оценки прочности материала при переменных напряжениях используется определяемая опытным путем характеристика – предел выносливости σ_r, который представляет собой наибольшее в алгебраическом смысле напряжение цикла, при котором образец выдерживает не разрушаясь неограниченно большое число циклов.

Практически установлено, что если стальной образец выдержал некоторое базовое числоциклов N_Б , и не разрушился, то он не разрушится и при любом другом большем числе циклов. Для стали и чугуна принимают N_Б=10⁷.

Для цветных металлов и сплавов пользуются лишь понятием предела ограниченной выносливости при NБ=10⁸, т.к. они при очень большом числе циклов могут разрушиться и при небольших напряжениях.

На величину предела выносливости σ_r влияют различные факторы:

1) Асимметрия цикла.

Минимальное значение имеет предел выносливости при симметричном цикле (r = -1). Он в несколько раз меньше предела прочности, например, для углеродистой стали σ_-1 ≈ 0,43 σ_в, для легированной стали σ_-1 ≈ 0,35 σ_в +120 МПа, для серого чугуна σ_-1 ≈ 0,45 σ_в.

2) Вид деформации.

При растяжении-сжатии предел выносливости σ_-1р=(0,7 – 0,8) σ_-1 .

При кручении - τ_-1 ≈ 0,58 σ_-1 .

3) Концентрация напряжений.

Снижение предела выносливости за счет наличия концентраторов на-пряжений (выточек, отверстий, шпоночных канавок, резких переходов от одних размеров детали к другим и др.) учитывается действительным коэффициентом концентрации напряжений к_σ (к_τ )>1. В неответственных расчетах и при отсут-ствии данных величину к можно определять по следующим эмпирическим со-отношениям:

а) при отсутствии острых концентраторов для детали с чисто обработанной поверхностью

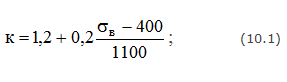
б) при наличии острых концентраторов напряжений

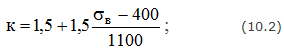
В приведенных соотношениях σ_в выражена в МПа. Эти формулы годятся для сталей с σ_в от 400 до 1300 МПа, и при их использовании не следует отдельно учитывать влияние качества поверхности детали.

4) Качество обработки поверхности учитывается при помощи коэффициента β >1, значение которого для различного качества обработки поверхности приводится в таблицах и графиках.

5) Абсолютные размеры детали учитываются при помощи так называемого масштабного фактора α_м>1. Значение α_м для различных материалов в зависимости от диаметра детали определяются из специальных графиков. Приближенно величины масштабного фактора для валов может быть вычислена по эмпирической зависимости

α_м = 1,2+0,1(d – 3), (10.3)

где d – диаметр вала в сантиметрах.

Совместное влияние концентрации напряжений, качества обработки поверхности и размеров детали оценивается коэффициентом

к_σ = к_σ · β · α_м . (10.4)

Расчет на прочность при переменных напряжениях (расчет на выносливость) на практике обычно выполняется как проверочный. Условие прочности принято записывать в виде

n ≥ [n], (10.5)

где [n] = 1,4 – 3,0 – нормативный коэффициент запаса усталостной прочности детали при данном цикле напряжений.

Коэффициент запаса по нормальным напряжениям определяется по формуле

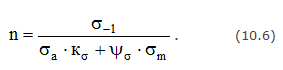
Здесь ψ - коэффициент, учитывающий влияние асимметрии цикла на предел выносливости. В случае, когда известна величина предела выносливости при пульсирующем цикле σ₀ ψ= (2 σ_-1 - σ₀)/σ₀. При отсутствии значений σ₀ ( τ₀ ) можно принимать ψ = σ_-1 /s, где s = 1400 МПа – для углеродистых и низколегированных сталей; s = 2000 МПа – для легированных сталей.

Наряду с коэффициентом запаса по усталостному разрушению должен быть определенкоэффициент запаса по текучести

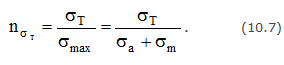
В качестве расчетного следует принять меньший из коэффициентов n_σ и n_σT.

Аналогично вычисляют и коэффициенты запаса по касательным напряжениям:

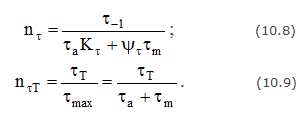
Для плоского напряженного состояния, когда действуют нормальные и касательные напряжения, коэффициент запаса определяется по эмпирической формуле

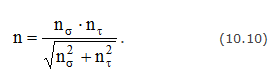
Оболочки и трубы