Допущения принятые в сопротивлении материалов

В сопротивлении материалов за расчетную модель принята модель идеализированного деформируемого тела и для решения поставленной задачи делается ряд допущений:

1. Материал тела представляет собой однородную сплошную среду. Физико-механические свойства тела одинаковы по всем направлениям (изотропная среда). Тела, у которых изменчивость механических свойств обусловлена неоднородностью структуры и спецификой изготовления, называются анизотропными, их свойства зависят от направления.

2. Материал до известного предела нагружения обладает идеальной упругостью.Упругостью называется способность материальных тел восстанавливать первоначальную форму и размеры тела после снятия нагрузки. Деформации, полностью исчезающие после снятия нагрузки, называются упругими в отличие от пластических, или остаточных, которые не исчезают.

3. Перемещения точек элемента (или системы элементов), обусловленные его деформацией, весьма малы по сравнению с размерами самого элемента. На основе этого допущения вводится принцип начальных размеров, согласно которому при составлении уравнений равновесия элемент или систему элементов рассматривают как недеформируемое тело. Такой подход позволяет пренебречь изменениями в расположении внешних сил при деформировании реального тела.

4. Перемещения точек элемента (системы элементов) в упругой стадии работы материала пропорциональны силам, вызывающим эти перемещения. Системы, подчиняющиеся такой закономерности, называются линейно-деформируемыми. Для них справедлив принцип независимости действия и сложения действия сил (принцип суперпозиции), который может быть сформулирован следующим образом: результат воздействия на тело системы сил равен сумме результатов воздействия отдельных составляю-щих этой системы, прикладываемых к телу последовательно и в любом порядке.

5. В теле до приложения нагрузки нет внутренних (начальных) усилий.

6. Деформации тела настолько малы, что можно не учитывать их влияние на взаимное расположение нагрузок.

7. Гипотеза плоских сечений. Поперечные сечения бруса плоские до приложения нагрузки остаются плоскими, и после приложения нагрузки.

8. Принцип Сен-Венана. В точках тела, достаточно удалённых от места приложения нагрузок, внутренние силы весьма мало зависят от конкретного способа приложения этих нагрузок. Этот принцип позволяет производить замену одной системы сил другой системой, статически эквивалентной, что может упростить расчёт.

Реальная конструкция и её расчётная схема

Реальные конструкции, как правило, характеризуются большой сложностью конструктивных форм (мост, купол и т.п.).

Провести расчёт реальных конструкции с учётом всех конструктивных особенностей очень часто сложно и иногда даже невозможно!

Вместе с тем конструктивные особенности не всегда оказывают существенное влияние на работу сооружения.

Поэтому при расчёте реальной конструкции её всегда заменяют идеализированной упрощённой схемой – так называемой расчётной схемой, выбор которой является исключительно ответственным этапом расчёта.

От этого выбора зависит точность и трудоёмкость расчёта. Иногда даже небольшое уточнение её ведёт за собой существенное усложнение расчёта или наоборот.

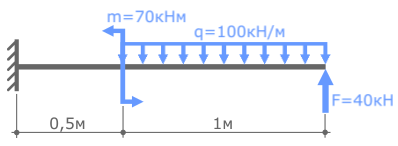
Пример расчетной схемы для решения задачи

Расчётная схема должна удачно отражать основной характер работы реальной конструкции, устраняя несущественные второстепенные факторы.

При схематизации реальных объектов основными элементами расчётных схем являются: брус, оболочка, конструкция крепления этих элементов, также делаются упрощения в системе сил, приложенных к элементу конструкции.