Основные инвестиционные задачи

Обычно рассматривают два вида инвестиций: реальные и финансовые. Реальные — это инвестиции в какой-либо тип материально осязаемых активов, таких, как земля, оборудование, заводы. Финансовые инвестиции представляют собой контракты, записанные на бумаге, например, обыкновенные акции и облигации. Оба вида инвестиций тесно взаимосвязаны. С обновлением и расширением основных фондов непосредственно связаны реальные инвестиции. Источником финансирования реальных инвестиций могут быть доходы, полученные от финансовых инвестиций. Реальные инвестиции — это долгосрочные инвестиции, предполагающие получение дохода через определенное время (несколько месяцев или лет) и в течение продолжительного времени, причем поступления доходов от инвестиций зависят от колебаний конъюнктуры рынка.

Фактор времени отражается в разной стоимости денежных средств, относящихся к различным моментам времени. Это объясняется тем, что имеющиеся в настоящий момент денежные средства могут быть инвестированы и принести доход в будущем. Поэтому денежные средства, не инвестированные сегодня, не принесут доход в будущем и со временем обесценятся.

Фактор риска выражается здесь в том, что эффективность инвестиционного проекта оценивается с определенной степенью вероятности.

При анализе доходности инвестиций требуется экономическое обоснование и прогнозирование будущих условий, поэтому инвестиционный анализ в значительной степени является прогнозным и в применяемых методиках учитываются фактор времени и фактор риска.

В конечном итоге все проблемы, возникающие в процессе инвестиционного анализа, можно свести к шести основным задачам, решаемым с помощью несложных математических функций. Каждая из функций строится на знании следующих исходных данных: процентной ставки; периода начисления; дохода от инвестиций.

Под процентной ставкой понимается относительная величина дохода за фиксированный отрезок времени, т. е. отношение дохода (процентных денег) к сумме долга за единицу времени [55, с. 13 ]. При определении ставки дохода на инвестиции как основного финансового критерия используется эффект сложного процента.

Период начисления — это временной интервал, к которому приурочена процентная ставка. В аналитических расчетах в качестве периода начисления применяется, как правило, год.

Доход от инвестиций определяется в процессе прогнозных аналитических расчетов.

Сформулируем основные инвестиционные задачи:

Задача 1. Чему будет равен доход на инвестиции через определенное количество лет (кварталов) при заданной процентной ставке и соответственно в какую сумму можно оценить инвестиции через определенный период?

Для решения этой задачи применяется математическая модель, называемая накопленной суммой единицы* или множителем наращения F₁.

* Здесь и в дальнейшем применяются названия функций по работе [52] из библиографического списка.

Для определения прироста суммы применяется формула расчета сложного процента:

где r — процентная ставка; п — период наращения.

Накопленная за период сумма S_n определяется как произведение начальной суммы инвестиций на функцию наращения.

Использование данной функции предполагает, что ежегодный доход от инвестиций реинвестируется или капитализируется.

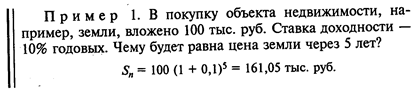
Задача 2. Доход от вложений равен 61,05 тыс. руб. Чему будет равна стоимость серии равных сумм вложений, депонированных в конце каждого из периодических интервалов? Для решения задачи применяется фактор накопления единицы за период — F₂:

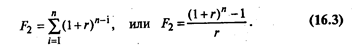
Накопления, полученные при депонировании вкладов в начале каждого периода, могут быть рассчитаны путем суммирования сложных процентов за весь рассматриваемый период.

Данная модель чаще применяется при определении доходности банковских операций с вкладами, но может использоваться и при оценке доходности реальных инвестиций.

Накопленная стоимость за период составит:

где a — аннуитет — денежный поток с равными поступлениями.

Задача 3. Чему равна текущая стоимость дохода, которая может быть получена от инвестиций в будущем?

Решение данной задачи позволяет привести доходы, полученные в будущем, к настоящему времени и сравнить сумму вложений в проект с доходом, полученным через определенный период времени.

Решается данная задача с применением факторного множителя, называемого текущей стоимостью единицы (реверсия). Текущая стоимость единицы (реверсия) — это величина, обратная накопленной сумме единицы.

При применении фактора текущей стоимости используется понятие дисконтирования, или ставки дисконта. Использование этого понятия вытекает из неравноценности затрат и результатов, осуществляемых и получаемых в различные моменты времени.

Для собственников капитала ставка дисконтирования идентифицируется с нормой дохода, ожидаемой от вложений капитала, поэтому чем больше шансы потерь, тем выше ставка дисконтирования, по которой разновременные доходы на инвестиции приводятся к моменту инвестирования.

Дисконтирование широко используется в практике зарубежных стран, где величину ставки дисконта (норматива приведения по фактору времени) связывают с риском деловых операций — см. табл. 16.1.

Приведение по фактору времени (дисконтирование) используется только в расчетах оценки эффективности вариантов инвестирования, но не учитывается при определении плановых и фактических показателей эффективности систем (прироста прибыли, снижения себестоимости и т.п.).

Сумма дисконта зависит от

• разрыва во времени между оттоком и притоком денежных средств;

• необходимой ставки процента или дисконта;

• риска вложений.

Фактор текущей стоимости (реверсия) рассчитывается по формуле:

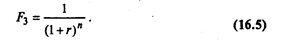
Текущая стоимость рассчитывается как произведение стоимости, прогнозируемой к получению в будущем, и фактора F₃.

Задача 4. Какую сумму следует вложить в проект, чтобы ежеквартально (ежегодно) получать определенный доход с учетом процентной ставки? Процентный доход предусматривается в размере, достаточном для возмещения потери стоимости во времени.

Алгоритм решения задачи идентичен определению текущей дисконтированной стоимости денежного потока, генерируемого в течение ряда равных периодов времени в процессе реализации какого-либо проекта. Отдельные элементы денежного потока относятся к разным временным интервалам, поэтому их суммирование искажает реальную доходность инвестиций. Приведение денежного потока к одному моменту времени осуществляется при помощи функции, называемой текущей стоимостью аннуитета:

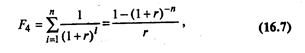
где п — количество периодов получения дохода от инвестиций.

Текущая стоимость аннуитетов определяется по формуле:

Формула (16.8) применяется для определения текущей стоимости, если доходы, получаемые за каждый i-й период, равны. При неравенстве доходов по временным периодам их получения рассчитывается дисконтированная стоимость за каждый период.

Задачи 3 и 4 наиболее часто применяются в анализе инвестиционных проектов.

Задача 5 является обратной задаче 4. Какой доход необходимо получать ежегодно, чтобы возместить (окупить) инвестиции за определенный период времени с учетом процентной ставки? Задача может быть поставлена так: какую сумму необходимо ежегодно (ежеквартально) вносить в банк для погашения кредита и процентов по нему?

Содержание задачи определяет название функции, применяемой для ее решения, — функция погашения кредита, которая определяется как величина, обратная текущей стоимости аннуитета:

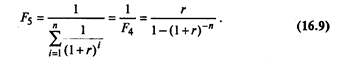
Ежегодный доход (аннуитет) определяется умножением суммы инвестиций на множитель F₅:

где IC — начальная сумма инвестиции (вложений).

Задача 6. Какую сумму следует ежегодно вкладывать на депозитный счет в банк, чтобы через определенное количество лет получить заданную стоимость?

Для решения задачи используется функция, называемая фактор фонда возмещения, — величина, обратная фактору накопления единицы за период:

Сумма ежегодного вклада составит:

где А — стоимость поступлений по истечении срока вложений.

Фактор фонда возмещения показывает денежную сумму, которую необходимо депонировать в конце каждого периода для того, чтобы через заданное число периодов остаток составил необходимую величину (например, 100 тыс. руб.). Данный фактор учитывает процент, получаемый по депозитам.

Часто в тех случаях, когда вплоть до истечения срока кредитного договора (долгового обязательства) кредитору выплачивается только процент, заемщики для погашения основной суммы кредита создают специальные фонды возмещения. В каждый период должник вносит в отдельный фонд сумму, которая вместе с начисляемым на нее процентом должна обеспечить погашение основной части кредита.

К одной из рассмотренных выше задач может быть сведена любая инвестиционная задача.