Частотные характеристики

Частотными характеристиками называются зависимости, связывающие входную и выходную величины линейной системы в установившемся режиме, когда входное воздействие изменяется по гармоническому закону x(t) = a sin wt с частотой и постоянной амплитудой a. На выходе системы после завершения переходного процесса устанавливается синусоидальные колебания y(t) = b sin(wt + j) . На комплексной плоскости входная и выходная величин для каждого момента времени t определены векторами а и b.

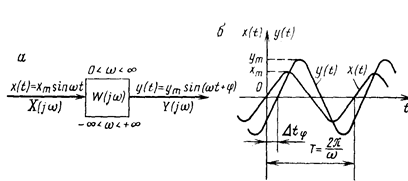
В комплексной тригонометрической форме

x = a(cos wt + j sin wt)

y = b[cos(wt + j) + j sin(wt + j)].

Используя формулу Эйлера e^jwt = cos wt + j sin wt, получим

x(t) = ae^jwt; y(t) = be^j(wt+j).

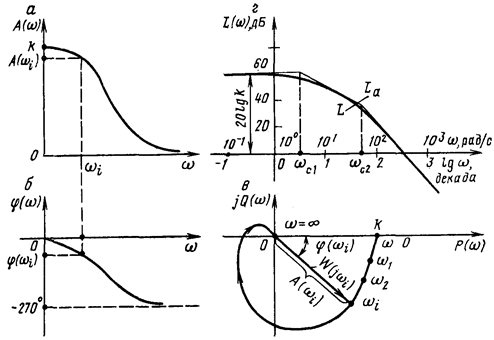
Если амплитуду колебаний входной величины оставить неизменной, а изменять частоту w от нуля до ¥, то каждому значению частоты будут соответствовать определенные значения амплитуды колебаний b и сдвига фазы j на выходе системы. Это значит, что отношение амплитуд и разность фаз являются функциями частоты, т.е:

b/a = A(w); j = j(w).

Рассмотренные выше временные, передаточные и частотные характеристики однозначно связаны меду собой прямым и обратным преобразованиями Лапласа и Фурье. Это отражено в таблице.

Таблица.

Взаимные соответствия динамических характеристик.

Характер-ки	h(t)	w(t)	W(p)	W(jw)
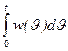
Переходная h(t)=			L-1{W(p)/p}	F-1{W(jw)/ jw}
Импульсная w(t)=	dh(t)/dt		L-1{W(p)}	F-1{W(jw)}
Передаточная W(p)=	pL{h(t)}	L{w(t)}		W(jw)½p=jw
Частотная W(jw)=	jwF{h(t)}	F{w(t)}	W(p)½p=jw