Основное уравнение измерений. Если физическая величина проявляется в отношениях эквивалентности, порядка и аддитивности, то она может быть: обнаружена

Если физическая величина проявляется в отношениях эквивалентности, порядка и аддитивности, то она может быть: обнаружена, классифицирована, проконтролирована и измерена.

Числа Q – это результаты измерений, совокупность которых должна обладать следующими свойствами:

1) Для проявления в отношении эквивалентности совокупность чисел Q, отображающая различные по размеру однородные величины, должна быть совокупностью одинаково именованных чисел. Это именование является единицей ФВ или ее доли. Единица физической величины [Q] — это ФВ фиксированного размера, которой условно присвоено числовое значение, равное единице и применяемое для количественного выражения однородных ФВ.

2) Для проявления в отношениях эквивалентности и порядка число q_{1 ,} отображающее большую по размеру величину Q₁ > Q₂ , выбирается большим, чем число q₂ , отображающее меньшую по размеру величину Q_2.

3) Для проявления в отношениях эквивалентности, порядка и аддитивности отвлеченное число, равное оценке суммарной измеряемой величины Q, возникающей в результате сложения составляющих однородных величин Q_i , должно быть равно сумме числовых оценок q_i этих составляющих.

Значение физической величины Q — это оценка ее размера в виде некоторого числа принятых для нее единиц.

Числовое значение физической величины q — отвлеченное число, выражающее отношение значения величины к соответствующей единице данной ФВ.

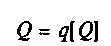-основное уравнение измерений.

Суть простейшего измерения состоит в сравнении ФВ Q с размерами выходной величины регулируемой многозначной меры q[Q]. В результате сравнения устанавливают, что q[Q] <Q <(q + 1)[Q].

Измерение — познавательный процесс, заключающийся в сравнении путем физического эксперимента данной ФВ с известной ФВ, принятой за единицу измерения.

Аксиомы метрологии:

1) Без априорной информации измерение невозможно

2) Измерение есть не что иное, как сравнение

3) Результат измерения является случайным.

Шкалы измерений

Разнообразные проявления (количественные или качественные) любого свойства образуют множества, отображения элементов которых на упорядоченное множество чисел или в более общем случае условных знаков образуют шкалы измерения этих свойств. Шкала измерений количественного свойства является шкалой ФВ. Шкала физической величины -— это упорядоченная последовательность значений ФВ, принятая по соглашению на основании результатов точных измерений.

В соответствии с логической структурой проявления свойств различают пять основных типов шкал измерений.

1. Шкала наименований (шкала классификации). Отображает качественные свойства элементов и характеризуется только отношением эквивалентности. В шкалах наименований отсутствует понятия нуля, "больше" или "меньше" и единицы измерения. Шкалы наименований - качественные. Примером шкал наименований являются атласы цветов, предназначенные для идентификации цвета.

2. Шкала порядка (шкала рангов). Для нее характерно отношение эквивалентности и порядка. Является монотонно возрастающей или убывающей и позволяет установить отношение больше/меньше между величинами, характеризующими указанное свойство.

Q₁>Q₂>…>Q_n

В шкалах порядка существует или не существует нуль, но принципиально нельзя ввести единицы измерения, так как для них не установлено отношение пропорциональности и соответственно нет возможности судить во сколько раз больше или меньше конкретные проявления свойства.

Примеры шкал порядка: шкалы измерений твердости, баллов силы ветра, землетрясений.

3. Шкала интервалов (шкала разностей). Применяются для объектов, свойства которых удовлетворяют отношениям эквивалентности, порядка и аддитивности. Шкала интервалов состоит из одинаковых интервалов, имеет единицу измерения и произвольно выбранное начало — нулевую точку. К таким шкалам относится летоисчисление по различным календарям, в которых за начало отсчета принято либо сотворение мира, либо рождество Христово и т.д. Температурные шкалы Цельсия, Фаренгейта и Реомюра также являются шкалами интервалов.

На шкале интервалов определены действия сложения и вычитания интервалов. По шкале времени интервалы можно суммировать или вычитать и сравнивать, во сколько раз один интервал больше другого, но складывать даты каких-либо событий просто бессмысленно.

Шкала интервалов величины Q описывается уравнением

Q = Q₀ + q[Q]

где q — числовое значение величины; Q₀ — начало отсчета шкалы; [Q] — единица рассматриваемой величины. Такая шкала полностью определяется заданием начала отсчета Q_o шкалы и единицы данной величины [Q].

4. Шкала отношений. Эти шкалы описывают свойства эмпирических объектов, которые удовлетворяют отношениям эквивалентности, порядка и аддитивности (шкалы второго рода аддитивные), а в ряде случаев и пропорциональности (шкалы первого рода — пропорциональные). В шкалах отношений существует естественный нуль и по согласованию устанавливается единица измерения.

Шкалы отношений — самые совершенные. Они описываются уравнением

Q = q[Q] ,

где Q — ФВ, для которой строится шкала,

[Q] — ее единица измерения, q — числовое значение ФВ. Переход от одной шкалы отношений к другой происходит в соответствии с уравнением q₂ = q₁ [Q₁]/[Q₂]

Примерами шкалы отношений являются шкала массы (второго рода) и термодинамическая температура(первого рода).

5.Абсолютные шкалы. Обладают всеми признаками шкал отношений, но дополнительно имеют естественное однозначное определение единицы измерения и не зависят от принятой системы единиц измерения. Такие шкалы соответствуют относительным величинам: коэффициенту усиления, ослабления, полезного действия и др. Для образования многих производных единиц в системе СИ используются безразмерные и счетные единицы абсолютных шкал.