Интерполяционный полином Ньютона

При построении интерполяционного полинома в форме Ньютона используется понятие разделенной разности, представляющее собой аналог понятия производной применительно к сеточным функциям.

Разделенной разностьюсеточной функции (табл. 8.1) нулевого порядкав узлах x_i , i = 0,…, n называются значения этой функции в этих узлах

f (x_i)= y_i , i = 0,…, n.

Определение 1. Разделенной разностьюсеточной функциипервого порядкав узлах x_i, i = 0,…, n-1 называют отношение

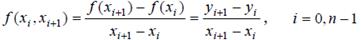
Определение 2. Разделенной разностью сеточной функции второго порядкав узлах x_i , i = 0,…, n-2называют отношение

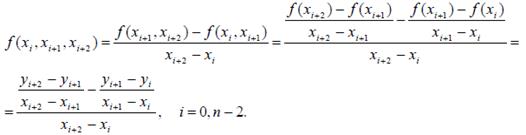
Определение 3. Разделенной разностью сеточной функции n-го порядкав узле x₀ называют отношение

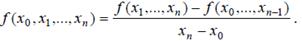
С использованием разделенных разностей интерполяционный полином Ньютона записывается в форме:

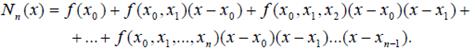(8.14)

Отметим, что при добавлении новых узлов первые члены многочлена Ньютона остаются неизменными.

Если функция задана в точках x₀, x₁,…, x_n, то при построении интерполяционного многочлена Ньютона удобно пользоваться таблицей, называемой таблицей разделенных разностей, пример которой для случая n =4приведен в табл. 8.2.

Таблица 8.2

Для повышения точности интерполяции в сумму (8.14) могут быть добавлены новые члены, что требует подключения дополнительных интерполяционных узлов. При этом безразлично, в каком порядке подключаются новые узлы. Этим формула Ньютона выгодно отличается от формулы Лагранжа.