Законы Ньютона и закон сохранения импульсов.
Закон Ньютона описывает взаимодействие двух тел между собой.
Он гласит:
Любые два тела взаимодействуют друг с другом с силами равными по величине, противоположными по направлению и приложены к различным телам.
Математически формулировка закона записывается
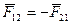
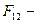 сила, с которой первое тело действует на второе.
сила, с которой первое тело действует на второе.
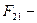 сила, с которой второе тело действует на первое.
сила, с которой второе тело действует на первое.
При этом эти силы приложены 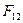 ко второму телу, а
ко второму телу, а 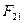 к первому телу.
к первому телу.
Поэтому их нельзя складывать и понятие равнодействующей этих сил не имеет смысла.
Отметим, что все три закона Ньютона, справедливы только в инерциальной системе отсчета.
Рассмотрим систему состоящую из нескольких тел, причем тела этой системы взаимодействуют только между собой – такая система тел называется ЗАМКНУТОЙ.
Эксперименты показывают, что суммарный импульс движения тел с течением времени не изменяется – ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
Математически закон сохранения импульса:
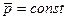 (2.12)
(2.12)
соотношение (2.12) можно получить при помощи второго и третьего закона Ньютона, если учесть, что суммарный импульс замкнутой системы находится как векторная сумма импульсов тел составляющих систему.
Рассмотрим систему состоящую из N-частиц (материальных точек). Обозначим через 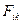 силу, с которой k-я частица действует на
силу, с которой k-я частица действует на
i-ю . 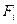 - результирующая всех внешних сил, действующих на i-ю частицу.
- результирующая всех внешних сил, действующих на i-ю частицу.
Уравнения движения всех N- частиц:
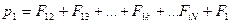
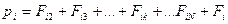
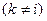
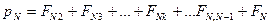
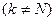
Сложим все уравнения, получится:
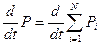
производная по времени.
Сумму внутренних сил можно представить в виде 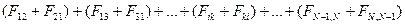
Согласно третьему закону Ньютона каждая из скобок =0 следовательно сумма внутренних сил, действующих на тела системы, всегда =0.
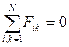 , с учетом этого получим
, с учетом этого получим
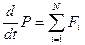 , таким образом производная по времени от суммарного импульса системы равна сумме внешних сил действующих на тела системы.
, таким образом производная по времени от суммарного импульса системы равна сумме внешних сил действующих на тела системы.
Если система замкнута, внешние силы отсутствуют и правая часть уравнения равна нулю. Соответственно 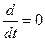 , следовательно p=const.
, следовательно p=const.
Рассмотрим применение закона сохранения импульса к так называемому неупругому удару.
Абсолютно неупругий удар- это такое взаимодействие тел, в результате которого тела движущиеся до взаимодействия раздельно движутся как одно целое.
Обозначим 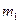 и
и 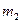 - массы тел
- массы тел
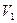 и
и 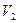 - скорости тел до соударения
- скорости тел до соударения
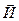 - скорость тел после соударения, тогда импульс системы этх двух тел равен:
- скорость тел после соударения, тогда импульс системы этх двух тел равен:
(2.13) 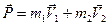 до соударения
до соударения
(2.14) 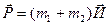 - после соударения
- после соударения
по закону сохранения импульса 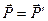 (2.15)
(2.15)
Подставим (2.13) и (2.14) в (2.15) к выражениям И
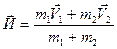 (2.16)
(2.16)
Отметим, что соотношение (2.16) это векторное соотношение, то есть в нем содержится три скалярных соотношения:
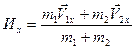 и т. д.
и т. д.
Одно из основных свойств массы, это то, что масса величина аддитивная (суммарная) это значит, что массу любого тела можно вычислить, как сумму масс частей составляющих это тело.
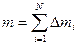 (2.17)
(2.17)
Такое разбиение бывает очень нужным в самых разнообразных случаях, один из них введение понятия центра масс.
По определению это точка, в которой сосредоточена масса всего тела (в котором можно считать сосредот.)
Для введения этого понятия тело мысленно разбивают на материальные точки, к каждой проводят r-вектор, а затем вычисляют r- вектор центра масс по формуле:
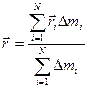 (2.18)
(2.18)
Выясним, что означают слова « в этой точке сосредоточенна масса всего тела». Это значит, что если к телу приложено множество сил к разным его точкам, то в результате, тело движется таким образом как будто к нему приложена одна сила, равная равнодействующей этих сил, причем эта сила приложена к центру масс (инерции) это утверждение называется ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС.
Докажем ее. Для этого, для каждой материальной точки запишем второй закон Ньютона: 
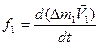
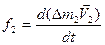 (2.19)
(2.19)
………………
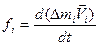
Суммируем уравнения из системы (2.19)
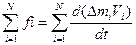 (2.20)
(2.20)
Учтем, что скорость 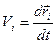 (2.21) будем считать, что масса каждой материальной точки
(2.21) будем считать, что масса каждой материальной точки 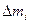 есть величина постоянная, тогда соотношение (2.20) можно переписать следующим образом.
есть величина постоянная, тогда соотношение (2.20) можно переписать следующим образом.
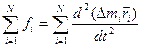 (2.22)
(2.22)
Меняя местами операции суммирования и дифференцирования:
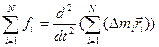 (2.23)
(2.23)
Выражение правой части под знаком суммы это числитель формулы r- вектора для центра масс. Поэтому можно формулу (2.23) преобразуем следующим образом. Умножить и разделить выражение под знаком производной на то выражение, которое стоит в знаменателе для r- вектора центра масс.
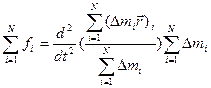
Теперь под знаком второй производной находится r- вектор центра масс.
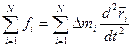 (2.24)
(2.24)
В левой части (2.24) находится равнодействующая всех сил действующих на тело. В правой части произведение всей массы тала на ускорение точки центра масс (инерции).
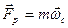
точка с – обозначает центр масс тела ч.т.д. Во многих задачах бывает удобно проводить решения в такой системе отсчета, в которой центр масс (инерции) покоится, называется система центра инерции (СЦИ).
2.6
Неинерциальные системы отсчета. Сила инертности.
В неинерциальной системе отсчета (НИСО), движущейся по отношению к инерциальным системам с ускорением тело будет иметь ускорение а, отличное от нуля. Поскольку в ИСО F=0, равенство F=ma не соблюдается. Система к является инерциальной. Показанные r – векторы связаны соотношением 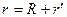






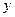
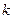
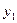
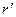 m
m
0 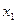
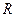
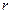
0 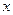
Двухкратное дифференцирование этого соотношения по времени приводит к
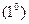
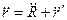 то есть
то есть 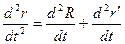
В случае , когда система 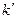 движется поступательно относительно к (то есть
движется поступательно относительно к (то есть 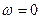 ),
), 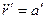 и соотношение
и соотношение 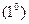 можно переписать
можно переписать 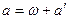 ;
; 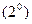
а- ускорение частицы в системе 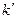 по отношению к системе к.
по отношению к системе к.
Умножим равенство 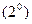 на массу частицы m, и согласно второму закону Ньютона произведение ma дает силу F, поэтому
на массу частицы m, и согласно второму закону Ньютона произведение ma дает силу F, поэтому
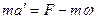
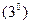
Таким образом, относительно системы 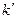 , частица ведет себя так, как если бы, кроме «реальной» силы F , на нее действовала дополнительная «фиктивная» сила
, частица ведет себя так, как если бы, кроме «реальной» силы F , на нее действовала дополнительная «фиктивная» сила 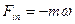 . Эта сила называется СИЛОЙ ИНЕРТНОСТИ. Сила инертности обусловлена свойствами той системы отсчета, в которой рассматриваются мех. явления.
. Эта сила называется СИЛОЙ ИНЕРТНОСТИ. Сила инертности обусловлена свойствами той системы отсчета, в которой рассматриваются мех. явления.
Использовав обозначение силы инертности, напишем уравнение 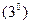
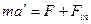
2.7 Момент силы и момент импульса. Уравнения движения и равновесия твердого тела (уравнеие моментов).
Важные законы динамики твердого тела связаны с положением момента силы. Существуют два различных понятия: момент силы, относительно точки, момент силы, относительно оси.
1. Пусть О некоторая точка, относительно которой вводится момент силы 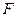 . Обозначим
. Обозначим 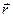 ,
, 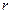 -вектор проведенный из точки О к точки приложения силы F. Тогда моментом силы обозн. Буква М, будет называться физ. Векторная величина, равная векторному произведению
-вектор проведенный из точки О к точки приложения силы F. Тогда моментом силы обозн. Буква М, будет называться физ. Векторная величина, равная векторному произведению 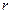 - вектора
- вектора 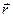 на силу F.
на силу F.
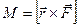 (2.26)
(2.26)



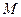
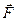
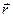
то есть направление моиента силы, находится по правилу векторного произведения, то есть все три вектора взаимно перпендикулярны. Мы ввели понятие момент силы, относительно точки О.
2. Моментом силы относительно оси проходящей через точку О, будет называться проекция момента силы относительно точки на эту ось , таким образом момент силы относительно точки это векторная величина и первичное понятие, а момент силы относительно оси величина скалярная и вторичное понятие.
Если через точку О проходит оси координат, то проекциями момента силы будут 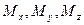 .
.
Они будут моментами силы относительно этих осей. В том случае когда необходимо находить момент нескольких сил относительно точки можно просто векторно сложить момент исходных сил. В том случае, когда линии действия сил лежат в одной плоскости, то момент этих сил относительно этой точки будет равен моменту равнодействующей этих сил относительно точки. Аналогично вводится понятие момента импульса относительно точки и момент импульса относительно оси.


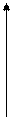
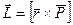 (2.27)
(2.27)
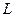
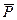
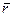
Пусть имеется материальная точка обладающая импульсом р, тогда моментом импульса относительно некоторой точки О, будет физическая величина равная векторному произведению 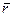 - вектора на импульс
- вектора на импульс 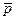 .
.
Моментом импульса относительно оси будет проекция вектора момента импульса относительно точки на ось проходящую через эту точку. Получим уравнение моментов для одной материальной точки. Для этого продифференцируем по времени соотношение (2.27)
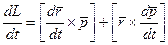 (2.28)
(2.28)
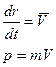 (2.29)
(2.29)
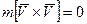 (2.30)
(2.30)
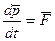 (2.31)
(2.31)
Подставляя эти уравнения в (2.28)
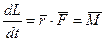 (2.32) уравнение моментов
(2.32) уравнение моментов
Где мы учли, что 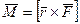
Уравнение связывает между собой момент силы действующей на материальную точку и скорость изменения момента импульса. Нетрудно увидеть, что формулы (2.31) и (2.32) очень похожи.
(2.31) выражает второй закон Ньютона, поэтому можно утверждать, что (2.32) тоже выражает второй закон Ньютона, записанный для моментов, то есть для вращательного движения. Если на твердое тело или точку внешние силы не действуют, или действуют таким образом, что их суммарный момент равен нулю, то тело или точка будут находиться в состоянии равновесия. Таким образом для тела или точки способных вращаться относительно некоторой точки или оси, уравнение равновесия будут иметь вид:
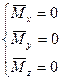 (2.34)
(2.34)
2.8
Момент инерции тела относительно оси.
Рассмотрим простейший случай вращательного движения твердого тела, а именно, когда имеется одна ось вращения ОО и тело вращается вокруг этой оси. В этом случае все точки тела движутся по окружностям, центры которой лежат на оси вращения, а радиусами окружности является расстояние от оси вращения до данной точки.


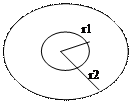 |
В этом случае моментом импульса относительно оси ОО, будет проекция момента импульса относительно любой точки лежащей на оси вращения на эту ось. Величина момента импульса относительно оси будет находиться:
L=r*p (2.34)
Такую формулу можно записать для любой материальной точки данного тела если масса материальной точки 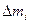 , то
, то
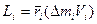 скалярная формула (2.35)
скалярная формула (2.35)
В данном случае 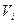 представляет собой линейную скорость точки
представляет собой линейную скорость точки 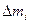 , движущейся по окружности радиусом
, движущейся по окружности радиусом 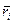 .
.
Если свести угловую скорость 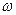
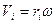 (2.36)
(2.36)
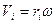
Подставим (2.36) в (2.35) получим
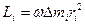 (2.37)
(2.37)
Введем новую физическую величину момент инерции (J) для материальной точки эта величина находится по формуле:
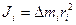 (2.38)
(2.38)
С учетом (2.38) выражение для момента импульса
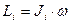 (2.39)
(2.39)
Если просуммировать соотношение (2.39) по всем индексам i, то получим:
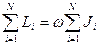 (2.40)
(2.40)
В левой части (2.40) находится момент импульса всего тела, а в правой части произведение угловой скорости на момент инерции всего тела:
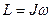 (2.41)
(2.41)
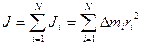 (2.42)
(2.42)
Формула (2.42) выражает значение момента инерции для любого мела, в общем случае эта формула приближенная, и она будет тем точнее, чем на более мелкие части мы разбиваем тело.
В пределе при 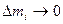 мы получим
мы получим
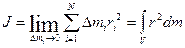 (2.43)
(2.43)
В данном случае интегрирование ведется по всему объему тела, что и отражено значком V , стоящему у интеграла.
Если ввести понятие плотности, то
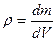
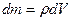
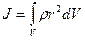 (2.44)
(2.44)
Рассмотрим, как находятся моменты инерции некоторых тел простых конфигураций.
Вывод для стержня, шара, диска.
Сплошной цилиндр (диск) 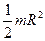
Шар 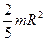
Прямой тонкий стержень 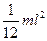 ось перпендикулярна стержню и проходит через середину.
ось перпендикулярна стержню и проходит через середину.
Стержень, ось перпендикулярна к стержню и проходит через его конец 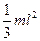
Сфера, ось проходит через центр 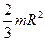 .
.
2.9
Установим законы механики, связывающие величины, характеризующие вращательное движение.
Пусть потенциальная энергия тела остается неизменной 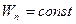 и изменяется только кинетическая энергия вращательного движения
и изменяется только кинетическая энергия вращательного движения 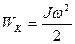 .
.
В соответствии с определение работы имеем:
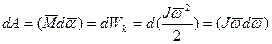
так как 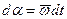 ,то следовательно
,то следовательно
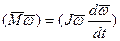
Из этого выражения легко получается закон:
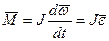
который похож на второй закон Ньютона. Он называется ОСНОВНЫМ ЗАКОНОМ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ:
момент силы, действующий на тело, есть величина, численно равная произведению момента инерции тела на его угловое ускорение.
Как и во втором законе Ньютона, можно учесть зависимость момента инерции тела от времени, и запишем в виде:
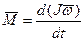
2.9
Вращательный момент и момент импульса основной закон динамики вращательного движения.
Т.о. момент инерции зависит от:
1. массы тела
2. геометрической формы тела
3. расп-ние масс
4. от положения оси вращения.
Последнее обстоятельство учитывается при помощи теоремы Штейнера.
Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси проходящей через центр масс параллельно данной и произведению массы тела на квадрат расстояния между осями.


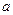
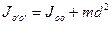
Доказать теорему самостоятельно, расстояние между а равно радиусу цилиндра r. Следовательно для однородного цилиндра:
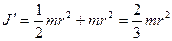
Стержень можно считать тонким, если max поперечный размер его много меньше длины l, следовательно
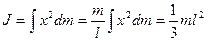
С помощью этой теоремы можно найти момент инерции 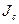 стержня относительно перпендикулярно к нему оси, проходящий через его центр.
стержня относительно перпендикулярно к нему оси, проходящий через его центр.
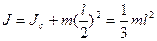
откуда 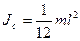 для стержня
для стержня
Формула Штейнера
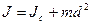
Доказательство теоремы:
Момент инерции J относительно оси О определяется выражением
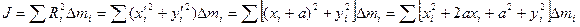 Разобьем это выражение на три суммы:
Разобьем это выражение на три суммы:
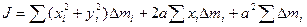
Первая сумма представляет собой момент инерции 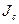 относительно оси, проходящей через центр масс. Сумма
относительно оси, проходящей через центр масс. Сумма 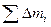 дает массу тела m. И сумма
дает массу тела m. И сумма 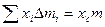 , где
, где 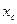 -координата центра масс, которая при сделанном выборе начала координат =0. Т.о. приходим к соотношению:
-координата центра масс, которая при сделанном выборе начала координат =0. Т.о. приходим к соотношению:
Глава 3.
Работа и механическая энергия. Законы сохранения импульса, момента импульса и энергии.
3.1
Закон сохранения импульса как фундаментальный закон природы. Реактивное движение.
Несмотря на то, что З.С.И. был нами получен при помощи второго закона Ньютона, на самом деле этот закон является фундаментальным законом природы, вытекающий из определенных свойствах пространства и времени. Этот закон справедлив, в отличие от закона Ньютона в любых системах отсчета, а не только в инерциальных и при любых взаимодействиях между телами.
Единственное ограничение выполнение которого необходимо для справедливости З.С.И. это ЗАМКНУТОСТЬ СИСТЕМЫ.
И даже это ограничение может быть нарушено, необходимо либо восстановить замкнутость, либо рассмотреть не выполняется ли условие замкнутости для некоторого выделенного направления.
В первом случае замкнутость системы восстанавливается путем включения в нее тех внешних тел, взаимодействие с которыми нарушало замкнутость.
Во втором случае необходимо найти такое направление вдоль которого выполняется условие замкнутости в том смысле, что равнодействующая всех сил действующих на эту систему, дает проекцию равно нулю на это направление.
В этом случае будет сохраняться не импульс системы, а только его проекция на данное направление.
В результате отдачи орудие приобретает некоторую скорость.




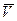
х
До выстрела все покоилось, суммарный импульс =0. В результате выстрела импульс стал равен:
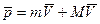
Если рассмотреть систему снаряд орудия с платформой, то она не замкнута, потому что платформа взаимодействует с Землей, но вдоль горизонтального направления система замкнута, поэтому ЗСИ выглядит:
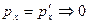 ;
; 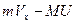
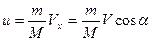
На выполнение ЗСИ основано особое движение в природе и технике, называют реактивным движением.
Реактивным называется движение возникающие в результате отделение тела и некоторых его частей с определенной скоростью. Если до этого тело покоилось, то в результате отделение тело начнет двигаться в сторону противоположную направлению скорости отделяющейся части тела.
Применим к этому случаю второй закон Ньютона
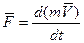 (3.1)
(3.1)
Важным признаком реактивного движения является то, что при этом меняется масса тела, поэтому второй закон Ньютона может быть записан:
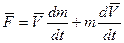 (3.2)
(3.2)
или
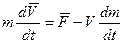 (3.3)
(3.3)
Из уравнения (3.3) следует что ускорение приобретаемое телом 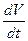 , обусловлено двумя факторами:
, обусловлено двумя факторами:
1. Действием на тело силы 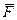
2. Изменением массы некоторого тела
Если скорость V, в данном случае скорость частиц отделяющихся от тела выразить через скорость самого тела, то уравнение
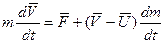
 (3.4)
(3.4)
V- скорость тела относительно неподвижной системы отсчета
U - скорость частиц отделяющихся от тела относительно неподвижной системы отсчета.
Уравнение (3.4) называется уравнением Мещерского.
Второе слагаемое часто обозначают:
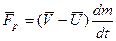 (3.5)
(3.5)
и называют РЕАКТИВНОЙ СИЛОЙ.
Если на тело не действуют внешние тела то уравнение (3.4) упрощается:
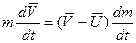 (3.6) уравнение Циолковского
(3.6) уравнение Циолковского
Эти уравнения описывают реактивное движение. Очень важной особенностью является то, что бы оно происходило необходимо взаимодействие с окружающей средой.
При помощи уравнения Циолковского вывести формулу для скорости ракеты.
Предположим сначала, что весь газ, образующийся при сгорании топлива, выбрасывается сразу, а не постепенно но, как это происходит в действительности. Обозначим массу газа через 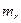 , а скорость газа
, а скорость газа 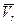 .
.
Массу и скорость оболочки обозначим соответственно 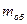 и
и 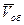 . Т.к. сумма импульсов оболочки и газа должна быть равна нулю, то нулю должна быть равна и сумма их проекций.
. Т.к. сумма импульсов оболочки и газа должна быть равна нулю, то нулю должна быть равна и сумма их проекций.
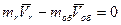 или
или
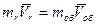 , отсюда
, отсюда
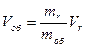
Скорость оболочки тем больше, чем больше скорость выбрасываемого газа и чем больше отношение массы газа к массе оболочки.
3.2
Закон сохранения момента импульса.
Запишем уравнение моментов
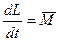 (3.7)
(3.7)
Если момент внешних сил действующих на данную систему =0, то такая система также называется ЗАМКНУТОЙ.
Условие замкнутости 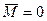 (3.8)
(3.8)
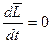 или
или 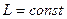 (3.9)
(3.9)
Соотношение (3.9) говорит о том, что момент импульса это величина сохраняющаяся, причем отметим, что соотношение (3.9) ВЕКТОРОНОЕ СООТНОШЕНИЕ, это означает, что сохраняются не только величина момента импульса, но и так же как ЗСИ, как и ЗСМИ. Является фундаментальным законом природы.
Его Выполнение можно связать с определенными свойствами пространства и времени. Рассмотрим, как выполняется ЗСИ на двух примерах:
Первый: 
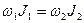
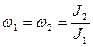
Второй: Гироскоп. Гироскопический эффект основан.



3.3
Движение в центральном поле. Законы Кеплера. Законы всемирного тяготения.
Центральным называется поле, котором силы, действующие со стороны поля, направлены к некоторой точке – центру.
Дата добавления: 2016-04-19; просмотров: 5568;
