Полемназывается особый вид материи, при помощи которой происходит взаимодействие удаленных друг от друга тел.
Понятие поле возникло благодаря концепции близкодействия, согласно которой взаимодействие удаленных тел происходит не непосредственно друг с другом, а благодаря возникновению особого вида материи, т.е. полю, которое служит передатчиком этого взаимодействия.
Рассмотрим движение планет солнечной системы в центре гравитационное поле, т.е. поле притяжения Солнца. Это движение изучалось астрономами, в результате Кеплер сформулировал три закона.
Первый: Все планеты солнечной системы движутся по эллипсам, в одном из фокусов которых находится Солнце.
Второй: Секториальная скорость планет есть величина постоянная.
Радиус-вектор каждой планеты за равные промежутки времени описывает равные площади.



 3
3
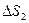
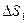
Отметим, что второй закон Кеплера является следствием закона сохранения момента количества движения.
Доказать.
Величина площади 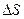 равна произведению основания треугольника Vdt , умноженному на половину высоты h, т.е. h/2.
равна произведению основания треугольника Vdt , умноженному на половину высоты h, т.е. h/2.
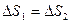
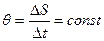 (3.10)
(3.10)
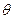 - секторная скорость
- секторная скорость
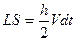 , но т.к.
, но т.к. 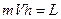 , то
, то 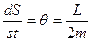 поэтому
поэтому 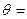 const , есть следствие того, что L=const .
const , есть следствие того, что L=const .
Если учесть , что Солнце-Планета есть механически изолированная система 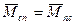 , то в такой системе момент количества движения
, то в такой системе момент количества движения
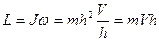 не изменяется. Вэтом заключается физический смысл второго закона Кеплера.
не изменяется. Вэтом заключается физический смысл второго закона Кеплера.
Третий: Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей и орбит.
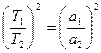 (3.11)
(3.11)
Анализируя законы Кеплера, Ньютон установил закон всемирного тяготения.
Предположим, что эллипсы, по которым движутся планеты вокруг Солнца очень близки к окружностям, тогда вместо больших полуосей в третий закон Кеплера войдут радиусы орбит.
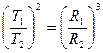 (3.12)
(3.12)
Ускорение, которое испытывают планеты будет центростримительные ускорения
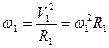 (3.13)
(3.13)
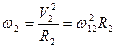
Запишем для двух планет закон Ньютона
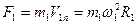
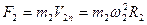 (3.14)
(3.14)
Разделим
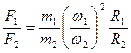 (3.15)
(3.15)
поскольку угловая скорость связана с периодом 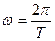 , то отношение
, то отношение
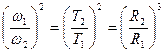 (3.17)
(3.17)
Такое отношение двух сил действует со стороны Солнца возможно только в том случае, когда каждая из этих сил прямо пропорциональна массе планеты, и обратно пропорциональна радиусу этой планеты.
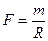 (3.18)
(3.18)
Если ввести коэф. Пропорциональности можно написать
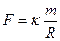
по третьему закону Ньютона, такая же сила должна действовать и со стороны планеты на Солнце.
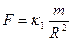
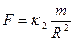 (3.19)
(3.19)
(3.18) и (3.19) совместно могут выполняться в том случае, когда
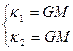 (3.20)
(3.20)
Т.о. сила взаимодействия между любой планетой и Солнцем находится по формуле:
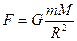 (3.21)
(3.21)
Планеты и солнце находящиеся друг от друга так далеко, что их можно считать материальными точками.
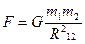 (3.22)
(3.22)
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ:
Любые две материальные точки притягиваются друг к другу силами прямопропорциональными произведению масс этих точек и обратно пропорционально квадрату расстояния между ними.
Эти силы направлены вдоль линии соединяющей материальные точки.



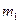
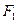
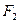
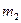
Для того, чтобы записать ЗВТ в векторной форме необходимо левую и правую часть (3.22) умножить.
Этот единичный вектор можно записать
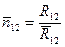
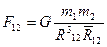
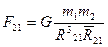
Эти формулы выражают закон всемирного тяготения в векторном виде.
Из них следует, что силы гравитационного взаимодействия двух материальных точек одинаковы по модулю, но противоположны по направлению. (т.е. подчиняются третьему закону Ньютона)
G-гравитационная постоянная
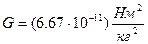
Для того, чтобы вычислить силу гравитационного взаимодействия двух тел произвольной формы необходимо мысленно разбить каждое из этих тел на материальные точки.
Найти силы каждой пары материальных точек, а затем векторно эти силы сложить в результате:
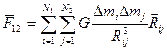 (3.24)
(3.24)
Для вычисления эту формулу не используют
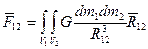 (3.25)
(3.25)
Если формулы (3.24) или (3.25) применить для расчета сил взаимодействия между шарами, но получится формула вида (3.23), в которой под расстоянием R, будет расстояние между центрами шаров.
Итак, формула ЗВТ вида (3.23) применима для расчета силы гравитационного притяжения в трех случаях:
1. Две материальные точки взаимодействуют
2. Взаимодействуют две однородные сферы (R-расстояние между центрами)
3. Взаимодействуют материальная точка и однородная сфера.
3.4 Работа и кинетическая энергия. Мощность.
Если на некоторое тело или материальную точку массой m, действует сила F и под действием этой силы совершается элементарное перемещение dS, то элементарной работой будет называться величина, численно равная произведению проекции силы на перемещение S,на величину перемещения
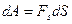 (3.26)
(3.26)
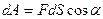 (3.27)
(3.27)



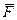


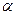
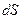
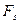
Если воспользоваться формулой скалярного произведения, то можно записать формулу:
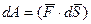 (3.28)
(3.28)
Для того, чтобы вычислить формулу на конечном перемещение необходимо это перемещение разбить на маленькие промежутки 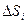 ,критерий малости этих промежутков таков в пределах
,критерий малости этих промежутков таков в пределах 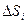 проекции силы
проекции силы 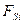 можно считать постоянной.
можно считать постоянной.
Далее вычисляется работа на всех 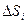 .
.
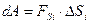
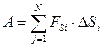
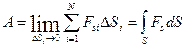 (3.29)
(3.29)
Итак,
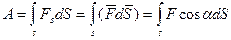 (3.30)
(3.30)
В соотношениях (3.30) все интегралы являются криволинейными интегралами, т.е. эти интегралы берутся вдоль траектории движения тела или точки.
Мощностью называется величина, которая характеризует скорость совершения работы.
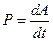 (3.31)
(3.31)
И работа и мощность являются величинами скалярными. Измеряются:
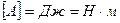
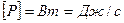
Если в (3.31) подставить (3.28)
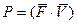 (3.32)
(3.32)
Если воспользоваться вторым законом Ньютона
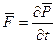
и формулой: 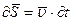
и подставить эти две формулы в (3.28), то получится:
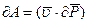 (3.33)
(3.33)
Воспользуемся выражением для импульса:
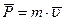
при этом 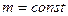
тогда: 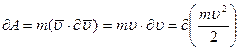 (3.34)
(3.34)
Дата добавления: 2016-04-19; просмотров: 577;
