Интерполяционный полином Лагранжа

Для полиномиальной интерполяции можно не решать СЛАУ (8.6), а записать многочлен (8.1) в специальной форме, одной из разновидностей которой является полином Лагранжа.

Пусть функция f(x) задана таблицей. Построим интерполяционный полином L_n(x), степени не больше n и для которого выполнены условия (8.8).

L_n(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ,

L_n(x₀) = y₀ , L_n(x₁) = y₁ , _…, L_n(x_n) = y_n . (8.8)

Лагранж предложил строить многочлен L_n(x) степени в виде:

L_n(x) = l₀(x) + l₁(x) +…+ l_n(x) (8.9)

где l_i(x) – полином степени n, причем

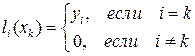(8.10)

Требование (8.10) совместно с выражением (8.9) обеспечивает выполнение условий (8.8).

Полиномы l_i(x) составим следующим образом:

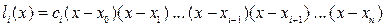(8.11)

Здесь в каждом полиноме l_i(x) отсутствует скобка (x - x_i), которой соответствует коэффициент c_i.

Найдем неизвестные коэффициенты c_i, i=0,…, n, называемые коэффициентами Лагранжа, используя условие L_n(x_i)=y_i, , i=0,…, n:

При x = x₀L_n(x₀) = y₀.

L_n(x₀) = c₀(x₀-x₁) (x₀-x₂) … (x₀-x_n) = y₀.

Следовательно, коэффициент c₀ вычисляется по следующей формуле:

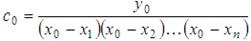
При x = x₁L_n(x₁) = y₁:

L_n(x₁) = c₁(x₀-x₁) (x₀-x₂) … (x₀-x_n) = y₁.

Следовательно, коэффициент с₁ вычисляется по следующей формуле:

.

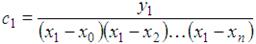Значения остальных коэффициентов вычисляются аналогично:

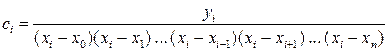
С учетом найденных коэффициентов интерполяционный многочлен Лагранжа запишется в виде

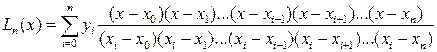. (8.12)

Хотя формула Лагранжа имеет не совсем привычную форму, тем не менее, это одна из форм записи полинома nстепени.

Пример 8.1. Построить интерполяционный полином Лагранжа для функции, заданной таблицей:

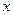
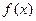
Решение

Из таблицы видно, что x₀ = 1, x₁ = 3, x₂ = 4, т. е. степень n интерполяционного полинома не выше, чем вторая. Используя формулу (8.12) получаем:

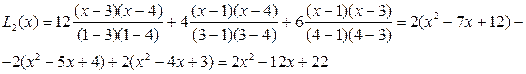
Формуле Лагранжа (8.12) можно придать более компактный (сжатый) вид.

Обозначим произведение:

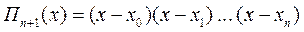
Продифференцировав это произведение по x, получим:

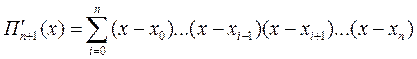
При x = x_i (i = 0, 1, …, n) имеем:

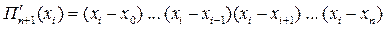
Тогда формула Лагранжа примет вид:

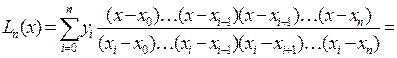
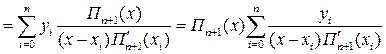
Окончательно:

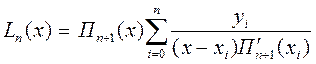(8.13)

Полином (8.13) называют интерполяционным полиномом Лагранжа n-й степени, т.к. он, во-первых, удовлетворяет условию интерполяции

L_n(x_i) = y_i , i = 0,…, n,

и, во-вторых, имеет n-ю степень.

С практической точки зрения интерес представляют два частных случая полинома Лагранжа:

· При n = 1 имеем две точки, поэтому в данном случае формула Лагранжа представляет уравнение прямой y = L₁(x), проходящей через две эти точки:

,

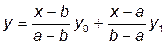где a и b — абсциссы этих точек.

· При n = 2 получим уравнение параболы y = L₂(x), проходящей через три точки

,

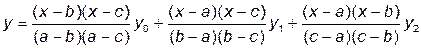где a, b и с — абсциссы этих точек.

Формула Лагранжа удобна для задачи интерполирования многих функций в одной точке x, т. к. все значения множителей L_k(x) можно вычислить однажды для всех функций.

Однако формула Лагранжа имеет существенный недостаток. Бывает, что заданное число узлов недостаточно для достижения заданной точности. Тогда к узлам, заданным в табл. 8.1, добавляют еще один или несколько узлов, что приводит к необходимости пересчета заново всех слагаемых в выражении 8.12 (или 8.13). Этого недостатка лишены интерполяционные полиномы Ньютона.