Методы Лагранжа и Эйлера

Описание законов движения может быть выполнено по методу Ж.Л. Лагранжа и Л. Эйлера.

Метод Лагранжа предполагает наблюдение за отдельными материальными объектами – частицами жидкости при их перемещении в пространстве. Итог наблюдений за конкретной частицей начальными координатами 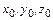(рис. 3.2.) при перемещении за время 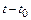является след 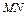, называемый траекторией.

Система функций геометрического характера

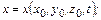
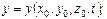(3.7)

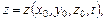
описывающих траекторию частиц, позволяет найти кинематические характеристики путем дифференцирования

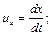
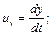
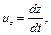(3.8)

а также вторые производные – ускорения

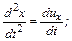
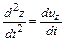(3.9)

Рис. 3.2. Характер движения жидкости

Метод Эйлера задает поле скоростей в рассматриваемой области движения жидкости. Полное описание задано, если скорости и давления определены в виде

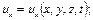
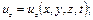(3.10)

линия, в каждой точке которой в данный момент времени вектор скорости направлен по касательной к ней, называется линией тока. Это основное понятие метода Эйлера. В случае неустановившегося движения в следующий момент движения через ту же точку будет проходить другая линия тока (рис.3.3 а).

Так как вектор 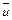с компонентами с элементами 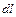с проекциями 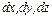на оси координат, то из условия параллельности векторов следует пропорциональность их проекций

(3.11)

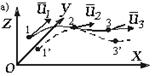
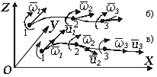
Рис. 3.3. Линия тока и линии завихренности

В случае установившегося движения линия тока сохраняет свое положение в пространстве и совпадает с траекторией.

Каждая частица вращается с угловой скоростью 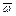. Линия, во всех точках которой направление векторов 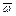совпадает с касательной к ней, является вихревой линией.

Из того, что вектор 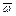с компонентами 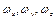совпадает по направлению с элементом длины вихревой линии 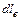, имеющим компоненты 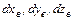, то уравнение вихревой линии имеет вид (рис. 3.3.б)

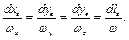(3.12)

Линии тока могут совпадать с линиями завихренности. Такое движение называется винтовым и определяется

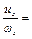
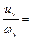
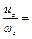
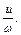(3.13)

Совокупность линий тока, проходящих через точки бесконечно малого замкнутого контура 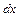, образует элементарную трубку тока (рис. 3.4 а).

Рис. 3.4. Трубка тока и вихревая трубка

Аналогичное образование в поле угловых скоростей называется вихревой трубкой.

Пучок линий тока, проходящих через все точки площадки 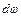, ограниченной контуром 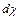называется элементарной струйкой.

Объем жидкости, проходящей через поперечное сечение 1 с площадью 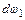за время 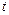должен равняться объему жидкости, прошедшему через любое сечение 2 с площадью 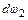за то же время в случае несжимаемой среды.