Метод Ньютона (метод касательных). В данном методе функция f(x) должна удовлетворять на отрезке (a,b) следующим условиям:
В данном методе функция f(x) должна удовлетворять на отрезке 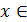 (a,b) следующим условиям:
(a,b) следующим условиям:
1) функция должна быть дважды дифференцируема;
2) 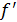 (x) ≠ 0; (*)
(x) ≠ 0; (*)
3) 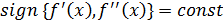 , на отрезке [a,b].
, на отрезке [a,b].
Итерационный алгоритм в методе Ньютона имеет вид
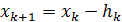 , k=0,1,2,… (3)
, k=0,1,2,… (3)
x0=b или x0=a,
где: xk – значение корня на k-ой итерации;
hk=? – корректирующая поправка xk на k-ой итерации.
Требуется определить hk.
Представим график функции f(x), удовлетворяющий условиям (*), на отрезке [a,b] на Рис.3
Пояснение метода Ньютона на Рис.3.
Рис.3. Метод Ньютона
Из 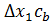 (прямоугольного) имеем
(прямоугольного) имеем 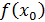 /
/ 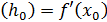 откуда
откуда 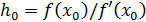 , тогда на основании (2а) имеем
, тогда на основании (2а) имеем
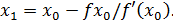
Аналогично из прямоугольного треугольника 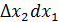 получаем
получаем
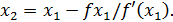
В общем случае для (k+1)-ой итерации можно записать
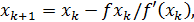 (3а)
(3а)
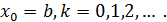
Сходимость итерационного алгоритма (2*) или (3а) очевидна.
Остановка итерационного алгоритма производится при выполнении условия 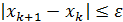 , а результатом является
, а результатом является 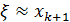 .
.
Достоинство – сходимость метода на порядок больше по сравнению с методом половинного деления.
Недостатки: – более жесткие требования к f(x) (смотри (*));
– в каждой итерации необходимо вычислять 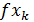 и
и 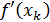
Дата добавления: 2016-03-04; просмотров: 431;
