ИССЛЕДОВАНИЕ ИНТЕРФЕРЕНЦИОННЫХ КОЛЕЦ НЬЮТОНА

Кольца Ньютона наблюдаются, когда выпуклая поверхность линзы L большого радиуса кривизны R соприкасается в некоторой точке с плоской поверхностью пластинки, так что остающаяся между ними воздушная прослойка постепенно утолщается от точки соприкосновения к краям (рис.1). Если на линзу падает пучок монохроматического света, то световые волны, отраженные от верхней и нижней границы этой воздушной прослойки, будут интерферировать между собой. При этом получается следующая картина: в центре - черное пятно, окруженное рядом концентрических светлых и черных колец убывающей ширины; цвет световых колец соответствует цвету монохроматического освещения. При наблюдении в проходящем свете картина будет обратная: пятно в центре станет светлым, все светлые кольца заменяются темными, и наоборот. Если падающий свет – белый, то вместо чередующихся черных и светлых колец возникает система разноцветных колец, повторяющихся периодически. Изменение цвета колец в каждом периоде имеет такую же последовательность, какая наблюдается в видимом спектре белого света – от фиолетового до красного.

Пусть AB (рис.2) представляет в сильно увеличенном виде небольшую часть нижней поверхности линзы L вблизи точки касания, а CD – часть поверхности плоской пластинки под ней. Два параллельных луча 1 и 2 попадают на воздушный слой в точках а и с. Толщину воздушного слоя между этими точками приблизительно можно считать одинаковой и равной d. Такое приближение допустимо потому, что R велико, и при малом расстоянии между точками а и с изменением толщины воздушного слоя можно пренебречь. Луч 1 после преломления в точках а и с и отражения от верхней плоскости пластинки Р в точке в встречается в точке с с отраженным лучом 2. Лучи интерферируют. Так как до точки с путь первого луча больше, чем путь второго, на расстояние (ав+вс), равное приблизительно 2d, то первый луч отстанет от второго на путь 2d.

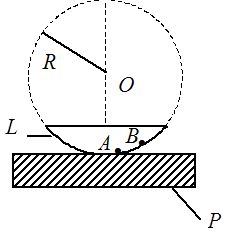
Рис. 1

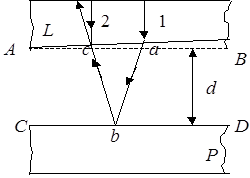
Рис.2

Кроме того, известно, что при отражении волн от среды оптически более плотной происходит потеря полуволны (1/2 λ). Следовательно, 1-й луч, дойдя до места встречи со 2-м лучом, отстанет от него на путь (2d- λ/2). Если эта разность хода окажется равной нечетному числу полуволн, то фазы колебаний у обоих лучей будут противоположны: лучи друг друга погасят, и в этом направлении мы будем наблюдать неосвещенное черное место. А там, где при другой толщине d разность хода окажется равной четному числу полуволн, фазы колебаний в обоих интерферирующих лучах будут одинаковы, и в соответствующем направлении мы увидим освещенное место. Так как толщина слоя воздуха, как это видно из рис.1, непрерывно возрастает, то и разность хода лучей будет меняться тоже непрерывно. Она будет делаться равной то четному числу полуволн, то нечетному, и, следовательно, мы будем наблюдать чередование освещенных мест с неосвещенными.

Геометрические места всех освещенных и неосвещенных точек определяются местами равной толщины воздушного слоя d и будут представлять собой концентрические окружности с центром в точке касания линзы с пластинкой (рис.­3). Радиус любого, например n-го, кольца, отсчитываемого от центра, можно легко определить (рис.4).Через R обозначен радиус кривизны линзы; d_n – толщина воздушного зазора, соответствующая рассматриваемому n-му кольцу; r_n-радиус кольца, n указывает порядковый номер кольца и может равняться 1, 2, 3 и т. д.

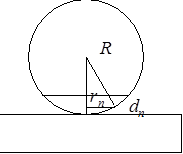
Рис. 3. Рис. 4

Из прямоугольного треугольника следует, что r_n² =R² –(R - d_n)² . Учитывая, что d«R, величиной d_n² по сравнению с 2Rd_n можно пренебречь. Тогда получается, что

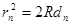^{. (11)}

Для светлого кольца разность хода интерферирующих лучей 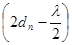должна равняться четному числу полуволн, т.е.,

,

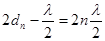где n-порядковый номер кольца. Отсюда .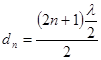

Подставляя это значение d_n в уравнение (11), найдем окончательное выражение для радиуса n-го светлого кольца.

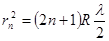. (12)

Чем больше n, тем меньше различие между радиусами соседних колец, т.е. тем теснее кольца.

Измеряя r_n , зная n и R, можно использовать уравнение (12) для определения длины волны монохроматического света λ. Но так как вследствие упругой деформации стекла невозможно добиться идеального соприкосновения сферической линзы и плоской пластинки в одной точке и касание происходит на каком-то конечном участке, то истинное значение n определить трудно. Чтобы получить более правильный результат, нужно вычислить λ по разности радиусов двух колец разных порядков. Тогда формула для определения λ будет иметь вид:

,

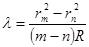где m и n – порядковые номера двух любых измеренных колец. Для расчета удобнее заменить радиусы диаметрами и переписать уравнение в окончательном виде:

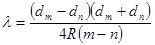. (13)

Полученное уравнение можно использовать также для определения радиуса кривизны линзы R:

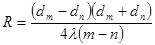. (14)

Длина волны λ должна быть известна.

Для темного кольца разность хода лучей должна равняться нечетному числу полуволн:

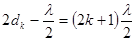, (15)

Где k – порядковый номер кольца. Отсюда для d_k получим формулу:

, .

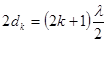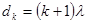Подставляя это значение d_k в (11), найдем выражение для радиуса k–го темного кольца

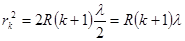. (16)

И для радиуса l–го темного кольца

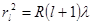, (17)

Из (16) и (17) следует

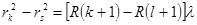
и

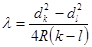. (18)

Если для отраженного света выполняется условие минимума (18), то это условие определяет условие максимума проходящего света.

Описание прибора.

В данной работе используется линза с относительно небольшим радиусом кривизны, и поэтому возникающие кольца Ньютона имеют настолько малые размеры, что рассмотреть их и измерить можно только под микроскопом.

На столик измерительного микроскопа помещается полированная пластинка из черного стекла, на которую кладется исследуемая линза.

К тубусу микроскопа привинчен вертикальный осветитель, представляющий собой небольшую трубку с боковым окном (рис.5). Внутри трубки, перед окном, находится стеклянная пластинка ab, установленная под углом 45⁰ к оси микроскопа. Свет от источника попадает на линзу после отражения от этой пластинки.

Для получения монохроматических колец используются фильтры. Стеклянный фильтр небольших размеров, пропускающий свет данной длины волны, помещается непосредственно на окуляр микроскопа. Для измерения радиуса колец в окуляре микроскопа имеется сетка, цена деления которой указана на микроскопе.

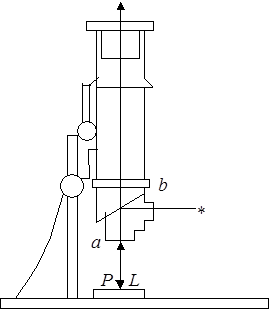
Рис.5