Линейные регрессионные модели с гетероскедастичными остатками
(1-5 стр Теория)
При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей 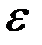 . В модели
. В модели
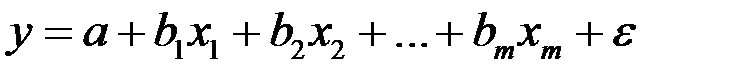
случайная составляющая 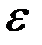 представляет собой ненаблюдаемую величину.
представляет собой ненаблюдаемую величину.
При изменении спецификации модели, добавлении в нее новых наблюдений выборочные оценки остатков 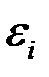 могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений
могут меняться. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений 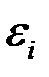 , т.е. остаточных величин.
, т.е. остаточных величин.
Делаются предположения относительно поведения остатков 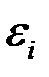 – остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию.
– остатки представляют собой независимые случайные величины и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию.
Исследования остатков 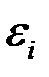 предполагают проверку наличия следующих пяти предпосылок МНК:
предполагают проверку наличия следующих пяти предпосылок МНК:
1) случайный характер остатков;
2) нулевая средняя величина остатков, не зависящая от 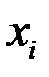 ;
;
3) гомоскедастичность – дисперсия каждого отклонения 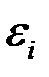 , одинакова для всех значений
, одинакова для всех значений 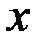 ;
;
Если распределение случайных остатков 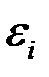 не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
не соответствует некоторым предпосылкам МНК, то следует корректировать модель.
Прежде всего, проверяется случайный характер остатков 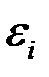 – первая предпосылка МНК. С этой целью стоится график зависимости остатков
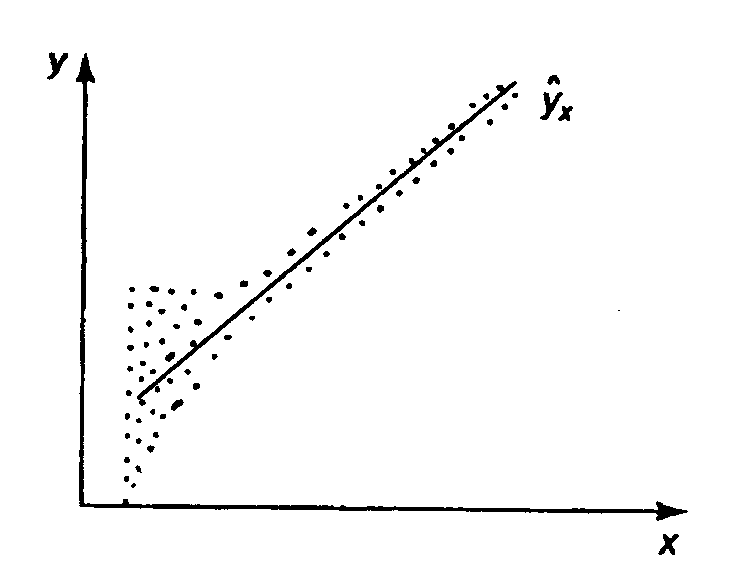
– первая предпосылка МНК. С этой целью стоится график зависимости остатков 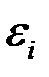 от теоретических значений результативного признака (рис. 2.1). Если на графике получена горизонтальная полоса, то остатки
от теоретических значений результативного признака (рис. 2.1). Если на графике получена горизонтальная полоса, то остатки 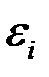 представляют собой случайные величины и МНК оправдан.
представляют собой случайные величины и МНК оправдан.

Рис. 2.1. Зависимость случайных остатков 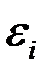 от теоретических значений
от теоретических значений 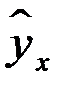 .
.
Возможны следующие случаи, если 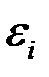 зависит от
зависит от 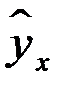 то:
то:
1) остатки 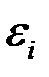 не случайны (рис. 2.2а);
не случайны (рис. 2.2а);
2) остатки 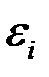 не имеют постоянной дисперсии (рис. 2.2б);
не имеют постоянной дисперсии (рис. 2.2б);
3) остатки 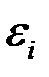 носят систематический характер (рис. 2.2в).
носят систематический характер (рис. 2.2в).
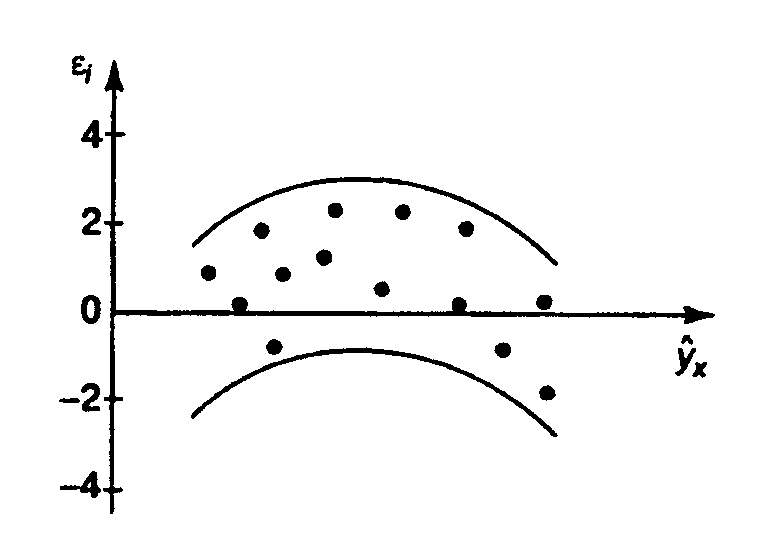
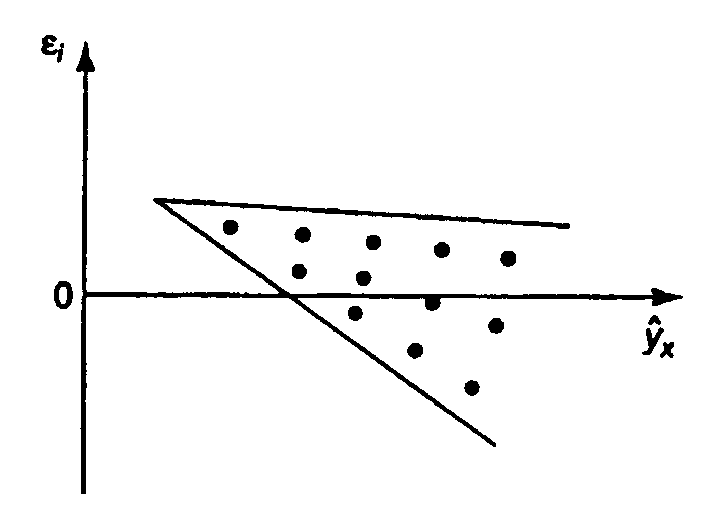
А б
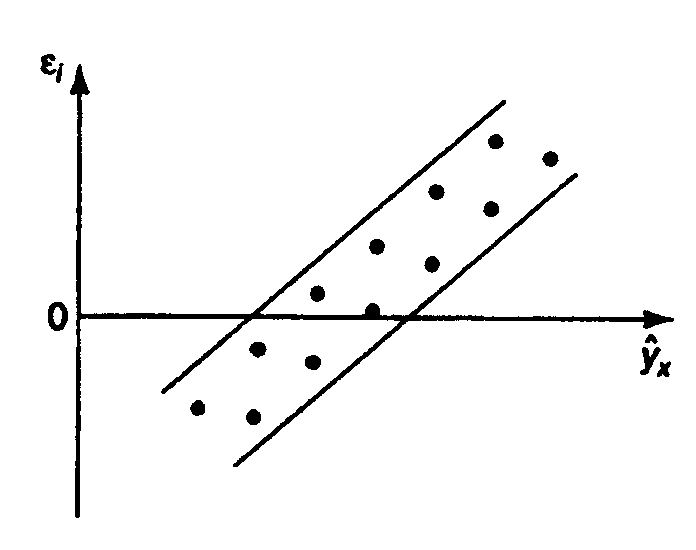
В
Рис. 2.2.Зависимость случайных остатков 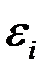 от теоретических значений
от теоретических значений 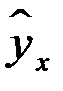 .
.
В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки 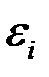 не будут случайными величинами.
не будут случайными величинами.
Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что 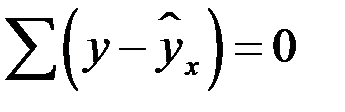 . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
. Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных.
Совершенно необходимым для получения по МНК состоятельных оценок параметров регрессии является соблюдение третьей предпосылки.
В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной (постоянной). Это значит, что для каждого значения фактора 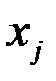 остатки
остатки 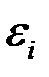 имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из графика зависимости (рис. 2.4).
имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Наличие гетероскедастичности можно наглядно видеть из графика зависимости (рис. 2.4).
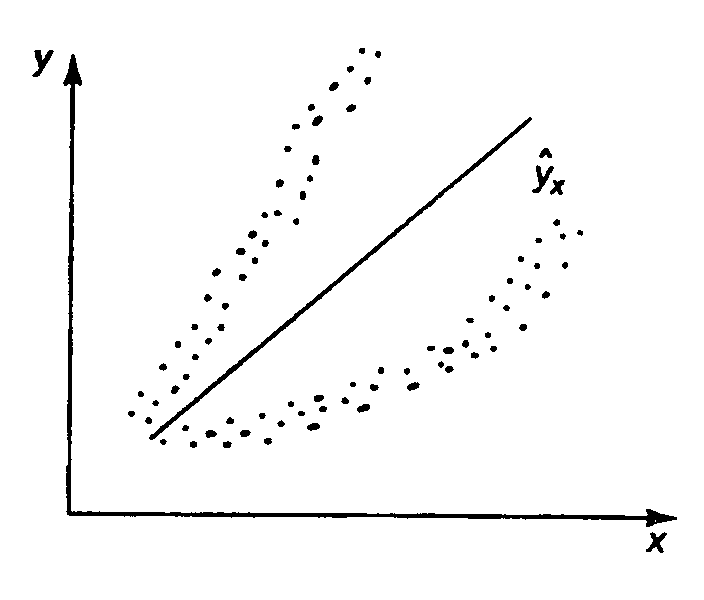
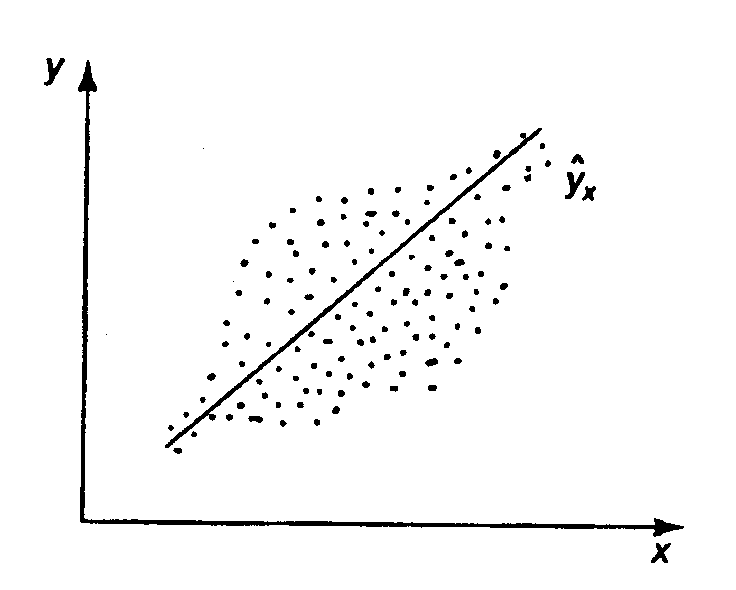
А б
В
Рис. 2.4. Примеры гетероскедастичности.
На рис. 2.4 изображено:
а – дисперсия остатков растет по мере увеличения 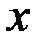 ;
;
б – дисперсия остатков достигает максимальной величины при средних значениях переменной 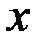 и уменьшается при минимальных и максимальных значениях
и уменьшается при минимальных и максимальных значениях 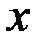 ;
;
в – максимальная дисперсия остатков при малых значениях 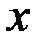 и дисперсия остатков однородна по мере увеличения значений
и дисперсия остатков однородна по мере увеличения значений 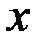 .
.
При несоблюдении основных предпосылок МНК приходится корректировать модель, изменяя ее спецификацию, добавлять (исключать) некоторые факторы, преобразовывать исходные данные для того, чтобы получить оценки коэффициентов регрессии.
При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастичности используют тест Гольфельда – Квандта.
Этапы теста:
1. упорядочить 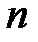 наблюдений по мере возрастания переменной
наблюдений по мере возрастания переменной 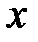 .
.
2. исключить из рассмотрения треть центральных наблюдений 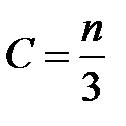 , тем самым, разделив совокупность на 2 группы соответственно с малыми и большими значениями переменной
, тем самым, разделив совокупность на 2 группы соответственно с малыми и большими значениями переменной 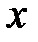 .
.
3. по каждой группе построить уравнение линейной регрессии.
4. определить остаточную сумму квадратов для первой группы 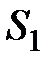 и второй группы
и второй группы 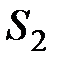 .
.
5. найти отношение 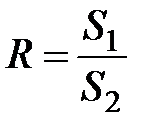 .
.
Если выполняется условие 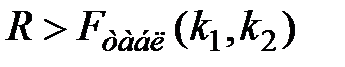 , где
, где 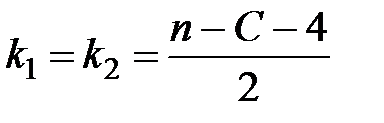 , то нарушается условие гомоскедастичности. Т.е. остатки в уравнении регрессии гетероскедастичны.
, то нарушается условие гомоскедастичности. Т.е. остатки в уравнении регрессии гетероскедастичны.
| <== предыдущая лекция | | | следующая лекция ==> |
| Психологические рекомендации по организации жизни подростков и юношей в детском доме. | | | Тема 7. ПОЛИГИБРИДНОЕ СКРЕЩИВАНИЕ |
Дата добавления: 2016-04-22; просмотров: 999;
