Дисперсия суммы случайных величин

Дисперсия суммы двух случайных величин равна сумме дисперсий и удвоенного корреляционного момента этих величин:

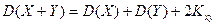. (4.5)

Доказательство.

Пусть X+Y=Z, тогда

,

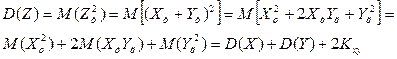что и требовалось доказать.

Формула (4.2) может быть обобщена на любое число слагаемых:

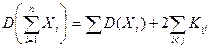, (4.6)

где 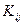- корреляционный момент случайных величин 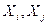, знак 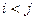под суммой обозначает, что суммирование распространяется на все возможные парные сочетания случайных величин .

Если случайные величины не коррелированны, то дисперсия суммы равна сумме дисперсий этих величин:

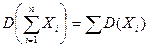. (4.7)

Справедливость равенства (4.7) вытекает из того, что для не коррелированных случайных величин корреляционный момент .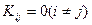

Дисперсия линейной функции случайных величинравна

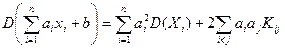, (4.8)

где 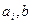- неслучайные величины.

Если случайные величины не коррелированны, то

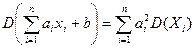. (4.9)

Пример. Определить дисперсию случайной величины 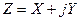, имеющей комплексный характер.

Дисперсией случайной комплексной величины называют МО квадрата модуля комплексной центрированной случайной величины, поэтому

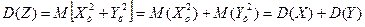. Следовательно, дисперсия комплексной случайной величины равна сумме дисперсий действительной X и мнимой Y случайных частей.

Дисперсия произведениядвух независимых случайных величин X и Y вычисляется по формуле

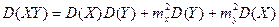. (4.10)

Доказательство.

Пусть 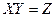, тогда

.

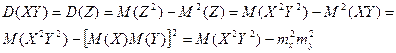Так как случайные величины X и Y независимы, то 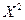и 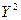также будут независимы, поэтому

.

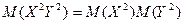Кроме того, .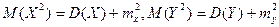

Следовательно,

,

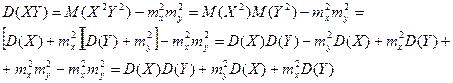что и требовалось доказать.

Дисперсия нелинейной функции случайных аргументов.Пусть случайная величина Z является функцией случайных аргументов 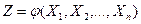. Требуется определить дисперсию D(Z).

В общем случае при решении этой задачи нелинейную функцию в окрестности точки 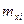линеаризуют разложением ее в ряд Тейлора:

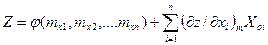. Применяя к этой случайной величине свойство дисперсии линейной функции и, учитывая, что дисперсия первого слагаемого (детерминированная функция) в этом выражении равна нулю, находим:

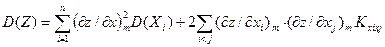. (4.11)