Закон сохранения импульса как фундаментальный закон природы. Реактивное движение
Несмотря на то, что З.С.И. был нами получен при помощи второго закона Ньютона, на самом деле этот закон является фундаментальным законом природы, вытекающий из определенных свойств пространства и времени. Этот закон справедлив, в отличие от закона Ньютона в любых системах отсчета, а не только в инерциальных и при любых взаимодействиях между телами. Единственное ограничение выполнение которого необходимо для справедливости З.С.И. это ЗАМКНУТОСТЬ СИСТЕМЫ. И даже это ограничение может быть нарушено, необходимо либо восстановить замкнутость, либо рассмотреть не выполняется ли условие замкнутости для некоторого выделенного направления.
В первом случае замкнутость системы восстанавливается путем включения в нее тех внешних тел, взаимодействие с которыми нарушало замкнутость.
Во втором случае необходимо найти такое направление вдоль которого выполняется условие замкнутости в том смысле, что равнодействующая всех сил действующих на эту систему, дает проекцию равно нулю на это направление.
В этом случае будет сохраняться не импульс системы, а только его проекция на данное направление.
В результате отдачи орудие приобретает некоторую скорость.




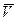
х
До выстрела все покоилось, суммарный импульс =0. В результате выстрела импульс стал равен:
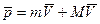
Если рассмотреть систему снаряд орудия с платформой, то она не замкнута, потому что платформа взаимодействует с Землей, но вдоль горизонтального направления система замкнута, поэтому ЗСИ выглядит:
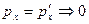 ;
; 
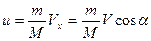
На выполнение ЗСИ основано особое движение в природе и технике, называют реактивным движением.
Реактивным называется движение возникающие в результате отделение тела и некоторых его частей с определенной скоростью. Если до этого тело покоилось, то в результате отделение тело начнет двигаться в сторону противоположную направлению скорости отделяющейся части тела.
Применим к этому случаю второй закон Ньютона
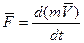 (3.1)
(3.1)
Важным признаком реактивного движения является то, что при этом меняется масса тела, поэтому второй закон Ньютона может быть записан:
 (3.2)
(3.2)
или
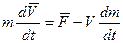 (3.3)
(3.3)
Из уравнения (3.3) следует что ускорение приобретаемое телом 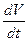 , обусловлено двумя факторами:
, обусловлено двумя факторами:
1. Действием на тело силы 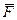
2. Изменением массы некоторого тела
Если скорость V, в данном случае скорость частиц отделяющихся от тела выразить через скорость самого тела, то уравнение
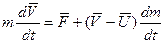
 (3.4)
(3.4)
V- скорость тела относительно неподвижной системы отсчета
U - скорость частиц отделяющихся от тела относительно неподвижной системы отсчета.
Уравнение (3.4) называется уравнением Мещерского.
Второе слагаемое часто обозначают:
 (3.5)
(3.5)
и называют РЕАКТИВНОЙ СИЛОЙ.
Если на тело не действуют внешние тела то уравнение (3.4) упрощается (уравнение Циолковского):
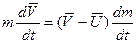 (3.6)
(3.6)
Эти уравнения описывают реактивное движение. Очень важной особенностью является то, что бы оно происходило необходимо взаимодействие с окружающей средой.
При помощи уравнения Циолковского вывести формулу для скорости ракеты.
Предположим сначала, что весь газ, образующийся при сгорании топлива, выбрасывается сразу, а не постепенно но, как это происходит в действительности. Обозначим массу газа через 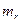 , а скорость газа
, а скорость газа 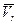 .
.
Массу и скорость оболочки обозначим соответственно 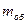 и
и 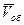 . Т.к. сумма импульсов оболочки и газа должна быть равна нулю, то нулю должна быть равна и сумма их проекций.
. Т.к. сумма импульсов оболочки и газа должна быть равна нулю, то нулю должна быть равна и сумма их проекций.
или 
отсюда 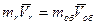 ,
,
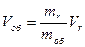
Скорость оболочки тем больше, чем больше скорость выбрасываемого газа и чем больше отношение массы газа к массе оболочки.
3.1. Закон сохранения момента импульса
Запишем уравнение моментов
 (3.7)
(3.7)
Если момент внешних сил действующих на данную систему =0, то такая система также называется ЗАМКНУТОЙ.
Условие замкнутости 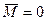 (3.8)
(3.8)
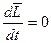 или
или 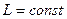 (3.9)
(3.9)
Соотношение (3.9) говорит о том, что момент импульса это величина сохраняющаяся, причем отметим, что соотношение (3.9) ВЕКТОРОНОЕ СООТНОШЕНИЕ, это означает, что сохраняются не только величина момента импульса, но и так же как ЗСИ, как и ЗСМИ. Является фундаментальным законом природы.
Его Выполнение можно связать с определенными свойствами пространства и времени. Рассмотрим, как выполняется ЗСИ на двух примерах:
Первый: 
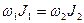
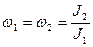
Второй: Гироскоп. Гироскопический эффект основан.


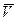
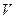
3.2. Движение в центральном поле. Законы Кеплера. Законы всемирного тяготения
Центральным называется поле, котором силы, действующие со стороны поля, направлены к некоторой точке – центру.
Полем называется особый вид материи, при помощи которой происходит взаимодействие удаленных друг от друга тел.
Понятие поле возникло благодаря концепции близкодействия, согласно которой взаимодействие удаленных тел происходит не непосредственно друг с другом, а благодаря возникновению особого вида материи, т.е. полю, которое служит передатчиком этого взаимодействия.
Рассмотрим движение планет солнечной системы в центре гравитационное поле, т.е. поле притяжения Солнца. Это движение изучалось астрономами, в результате Кеплер сформулировал три закона.
Первый: Все планеты солнечной системы движутся по эллипсам, в одном из фокусов которых находится Солнце.
Второй: Секториальная скорость планет есть величина постоянная.
Радиус-вектор каждой планеты за равные промежутки времени описывает равные площади.




 3
3
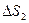
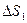
Отметим, что второй закон Кеплера является следствием закона сохранения момента количества движения.
Доказать.
Величина площади 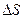 равна произведению основания треугольника Vdt , умноженному на половину высоты h, т.е. h/2.
равна произведению основания треугольника Vdt , умноженному на половину высоты h, т.е. h/2.
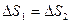
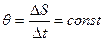 (3.10)
(3.10)
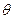 - секторная скорость
- секторная скорость
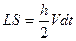 , но т.к.
, но т.к. 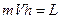 , то
, то 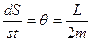 поэтому
поэтому 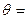 const , есть следствие того, что L=const .
const , есть следствие того, что L=const .
Если учесть , что Солнце-Планета есть механически изолированная система 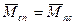 , то в такой системе момент количества движения
, то в такой системе момент количества движения
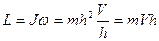 не изменяется. Вэтом заключается физический смысл второго закона Кеплера.
не изменяется. Вэтом заключается физический смысл второго закона Кеплера.
Третий: Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей и орбит.
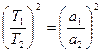 (3.11)
(3.11)
Анализируя законы Кеплера, Ньютон установил закон всемирного тяготения.
Предположим, что эллипсы, по которым движутся планеты вокруг Солнца очень близки к окружностям, тогда вместо больших полуосей в третий закон Кеплера войдут радиусы орбит.
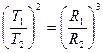 (3.12)
(3.12)
Ускорение, которое испытывают планеты будет центростримительные ускорения
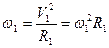 (3.13)
(3.13)
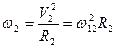
Запишем для двух планет закон Ньютона
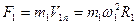
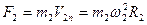 (3.14)
(3.14)
Разделим
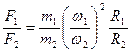 (3.15)
(3.15)
поскольку угловая скорость связана с периодом 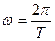 , то отношение
, то отношение
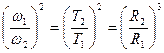 (3.17)
(3.17)
Такое отношение двух сил действует со стороны Солнца возможно только в том случае, когда каждая из этих сил прямо пропорциональна массе планеты, и обратно пропорциональна радиусу этой планеты.
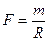 (3.18)
(3.18)
Если ввести коэф. Пропорциональности можно написать
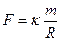
по третьему закону Ньютона, такая же сила должна действовать и со стороны планеты на Солнце.
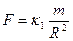
 (3.19)
(3.19)
(3.18) и (3.19) совместно могут выполняться в том случае, когда
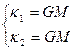 (3.20)
(3.20)
Т.о. сила взаимодействия между любой планетой и Солнцем находится по формуле:
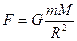 (3.21)
(3.21)
Планеты и солнце находящиеся друг от друга так далеко, что их можно считать материальными точками.
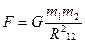 (3.22)
(3.22)
ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ:
Любые две материальные точки притягиваются друг к другу силами прямопропорциональными произведению масс этих точек и обратно пропорционально квадрату расстояния между ними.
Эти силы направлены вдоль линии соединяющей материальные точки.



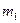
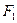
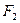
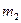
Для того, чтобы записать ЗВТ в векторной форме необходимо левую и правую часть (3.22) умножить.
Этот единичный вектор можно записать
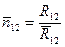
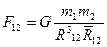
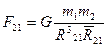
Эти формулы выражают закон всемирного тяготения в векторном виде.
Из них следует, что силы гравитационного взаимодействия двух материальных точек одинаковы по модулю, но противоположны по направлению. (т.е. подчиняются третьему закону Ньютона)
G-гравитационная постоянная
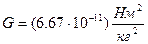
Для того, чтобы вычислить силу гравитационного взаимодействия двух тел произвольной формы необходимо мысленно разбить каждое из этих тел на материальные точки.
Найти силы каждой пары материальных точек, а затем векторно эти силы сложить в результате:
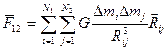 (3.24)
(3.24)
Для вычисления эту формулу не используют
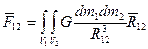 (3.25)
(3.25)
Если формулы (3.24) или (3.25) применить для расчета сил взаимодействия между шарами, но получится формула вида (3.23), в которой под расстоянием R, будет расстояние между центрами шаров.
Итак, формула ЗВТ вида (3.23) применима для расчета силы гравитационного притяжения в трех случаях:
1. Две материальные точки взаимодействуют
2. Взаимодействуют две однородные сферы (R-расстояние между центрами)
3. Взаимодействуют материальная точка и однородная сфера.
3.3. Работа и кинетическая энергия. Мощность
Если на некоторое тело или материальную точку массой m, действует сила F и под действием этой силы совершается элементарное перемещение dS, то элементарной работой будет называться величина, численно равная произведению проекции силы на перемещение S,на величину перемещения
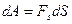 (3.26)
(3.26)
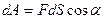 (3.27)
(3.27)



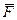


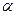

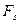
Если воспользоваться формулой скалярного произведения, то можно записать формулу:
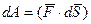 (3.28)
(3.28)
Для того, чтобы вычислить формулу на конечном перемещение необходимо это перемещение разбить на маленькие промежутки 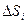 ,критерий малости этих промежутков таков в пределах
,критерий малости этих промежутков таков в пределах 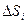 проекции силы
проекции силы 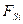 можно считать постоянной.
можно считать постоянной.
Далее вычисляется работа на всех 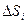 .
.
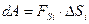

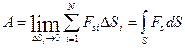 (3.29)
(3.29)
Итак,
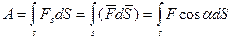 (3.30)
(3.30)
В соотношениях (3.30) все интегралы являются криволинейными интегралами, т.е. эти интегралы берутся вдоль траектории движения тела или точки.
Мощностью называется величина, которая характеризует скорость совершения работы.
 (3.31)
(3.31)
И работа и мощность являются величинами скалярными. Измеряются:
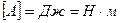
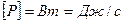
Если в (3.31) подставить (3.28)
 (3.32)
(3.32)
Если воспользоваться вторым законом Ньютона
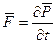
и формулой: 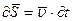
и подставить эти две формулы в (3.28), то получится:
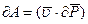 (3.33)
(3.33)
Воспользуемся выражением для импульса:

при этом 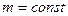
тогда: 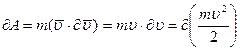 (3.34)
(3.34)
Таким образом можно ввести новую величину, обозначенную
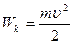 (3.35)
(3.35)
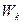 - кинетическая энергия, элементарное изменение которой равно элементарной работе, т. е.
- кинетическая энергия, элементарное изменение которой равно элементарной работе, т. е.
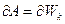 (3.36)
(3.36)
Если проинтегрировать левую и правую части, то получим:
 (3.37)
(3.37)
Это означает, что работа, совершаемая телом идет на увеличение кинетической энергии. Причем надо учесть, что в данном случае речь идет о работе всех сил, и внешних и внутренних.
Кинетическая энергия, как и работа измеряется в Дж:
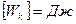
3.4. Связь между кинетической энергией в различных системах отсчета
Поскольку скорость движения есть величина относительная, зависящая от выбора системы отсчета, то кинетическая энергия также зависит от выбора системы отсчета. Скорость относительного движения равна 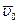 , тогда скорость движения материальной точки в одной системе отсчета будет
, тогда скорость движения материальной точки в одной системе отсчета будет 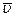 , а в другой
, а в другой  :
:
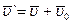 (3.38)
(3.38)
Соответственно:
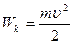 (3.39)
(3.39)
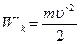 (3.40)
(3.40)
подставим (3.38) в (3.40), тогда с учетом (3.39)
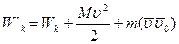 (3.41)
(3.41)
Формула (3.41) выражает связь между кинетической энергией материальной точки в двух различных системах отсчета.
Точно такое же соотношение можно было бы записать и для твердого тела, разбив его на материальные точки, записав для каждой материальной точки уравнение (3.41), а затем просуммировать по всем материальным точкам на которое разбито тело.
Если обозначить 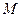 - массу всего тела, то формула (3.41) принимает вид:
- массу всего тела, то формула (3.41) принимает вид:
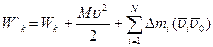 (3.42)
(3.42)
Если тело движется поступательно, то скорость движения всех его точек равны по величине и направлению, и тогда формула (3.42) упрощается:
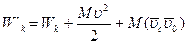 (3.43)
(3.43)
 - скорость движения центра масс.
- скорость движения центра масс.
Если в качестве одной из систем отсчета выбрать систему отсчета центра масс, то это значит 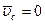 , и формула (3.43) упрощается:
, и формула (3.43) упрощается:
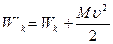 (3.44)
(3.44)
Формула (3.43) выражает собой теорему Кенига.
Теорема Кенига: Кинетическая энергия твердого тела в одной системе отсчета равна кинетической энергии этого тела в другой системе отсчета, сложенной с кинетической энергией относительного движения тела одной системы отсчета относительно другой.
3.5. Кинетическая энергия движения тела, как целого. Энергия вращающегося тела
Рассмотрим твердое тело участвующее одновременно в двух движениях: поступательном и вращательном.
Это означает, что каждая точка этого тела имеет две скорости, одна из которых обусловлена поступательным движением, а вторая - вращательным.
Выделим вращательное движение твердого тела и найдем кинетическую энергию соответствующую этому движению.
Для этого мысленно разобьем тело на точки.
Кинетическая энергия каждой точки:
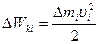 (3.45)
(3.45)
Где скорость  (3.46)
(3.46)
Тогда 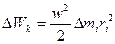 (3.47)
(3.47)
Т. к. момент инерции для каждой точки равен:
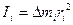 (3.48)
(3.48)
то 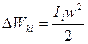 (3.49)
(3.49)
Для этого тела:
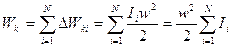 (3.50)
(3.50)
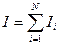
 (3.51)
(3.51)
Мы получили формулу для кинетической энергии вращательного движения твердого тела.
Общая кинетическая энергия будет находятся по формуле:
 (3.52)
(3.52)
Если тело находится без проскальзывания (пробуксовки) и является сферически симметричным, то между скоростью его поступательного движения и угловой скоростью существует обычная связь:
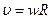 (3.53)
(3.53)
и тогда, зная формулу для момента инерции, можно упростить формулу (3.52).
Для шара: 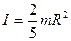
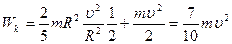 (3.54)
(3.54)
Из этого следует, что кинетическая энергия катящегося тела больше, чем этого же тела движущегося поступательно.
3.6. Консервативные и неконсервативные силы. Потенциальная энергия
Среди всех сил используемых в механике выделяется особый класс сил так называемые консервативные силы.
Это силы, работа которых не зависит от формы траектории по которой перемещается тело, а зависит только от начального и конечного положения тела.
Рассмотрим, например, работу силы тяжести:
Пусть тело массой 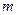 , перемещается из точки 1 в точку 2, под действием силы тяжести.
, перемещается из точки 1 в точку 2, под действием силы тяжести.
В каждой точке сила тяжести направлена вертикально.
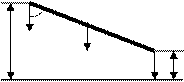 1
1
h1 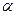
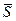 2
2
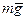
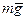
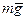 h2
h2
Тогда работа силы тяжести может быть найдена по формуле:
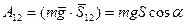 (3.55)
(3.55)
Будем считать, что ·1 находится на некоторой высоте h1, а ·2 - h2 от произвольного нулевого уровня.
Тогда формула (3.55) принимает вид:
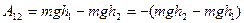 (3.56)
(3.56)
Формула (3.56) означает, что работа силы тяжести равна уменьшению некоторой новой величины, которая называется ПАОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ.
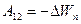 (3.57)
(3.57)
Потенциальная энергия силы тяжести:
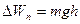 (3.58)
(3.58)
Таким образом, сила тяжести - это консервативная сила, которая обладает потенциальной энергией.
Если ввести ось z, направленную вертикально вверх, то можно показать, что:
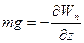 (3.59)
(3.59)
На этом примере получены формулы, справедливые для всех консервативных сил, т. е. работа любой консервативной силы F будет равна убыли (уменьшению) потенциальной энергии, которой обладает тело, благодаря действию на него данной силы.
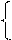
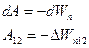 (3.60)
(3.60)
Кроме того, если потенциальная энергия зависит от координат x, y, z, то можно записать формулы:
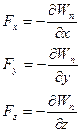 (3.61)
(3.61)
которые выражают проекции силы.
Вывести формулы для 2х потенциальных энергий:
1) гравитационного притяжения 2х точек.
2) силы упругости?
1) Когда 1я частица неподвижна и находится в начале координат, можно записать:
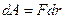
F - центральная сила, действующая на эту частицу.
r - радиус вектор этой точки.
А - работа внешних сил.
Если частица притягивается к силовому центру, работа на произвольном пути от точки 1 до точки 2, определяется выражением:
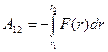
приняв эту работу убыли потенциальной энергии:
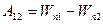
получим:  (10)
(10)
в случае гравитационного притяжения частиц
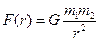
получаем: 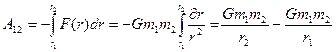 (20)
(20)
Сопоставление (10) и (20) дает для потенциальной энергии гравитационного взаимодействия 2х частиц выражение:
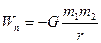
2) Установить, что как для растяжения, так и для сжатия пружины на величину х нужно совершить работу:
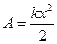
Эта работа идет на приращение потенциальной энергии пружины от удлинения х, и имеет вид:
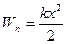
Если в результате действия консервативной силы, тело возвращается в исходную точку, т. е. работа совершается по замкнутому контуру, ясно, что такая работа будет равна нулю:
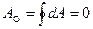 (3.62)
(3.62)
 - работа по замкнутому контуру.
- работа по замкнутому контуру.
Соотношение (3.62) также является критерием того, что силы совершающие работу А - консервативны.
Все остальные силы, которые не являются консервативными, являются неконсервативными.
Примеры неконсервативных сил:
1) диссипативные (рассеянные);
2) силы трения или сопротивления.
3.7. Закон изменения и сохранения механической энергии. Абсолютно упругий удар
Из выражений для работы силы тяжести, упругости и тяготения следует, что изменение потенциальной энергии равно работе консервативных сил с противоположным знаком:
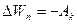
Для системы тел представим работу всех сил (А) в виде суммы работ консервативных сил (Ак), неконсервативных сил (Ан) и внешних сил (Ав):
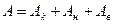
Следовательно:
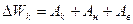
т. к. изменение полной механической энергии:
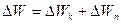
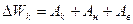
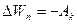 ,
,
то 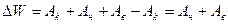
 - механическую энергию работа консервативных сил не меняет.
- механическую энергию работа консервативных сил не меняет.
Система тел консервативна, если среди внутренних сил системы отсутствуют неконсервативные силы. Для консервативных систем тел 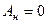 , а в замкнутой системе тел
, а в замкнутой системе тел 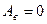 .
.
Закон сохранения механической энергии: механическая энергия консервативной замкнутой системы тел не изменяется при всех процессах, происходящих в системе.
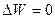
или 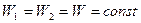
W=[Н×м]=Дж
Рассмотрим такое взаимодействие двух тел, в результате которого кинетическая энергия тел до взаимодействия равна кинетической энергии после взаимодействия. Такое взаимодействие будем называть АБСОЛЮТНО УПРУГИМ УДАРОМ.
Обозначим 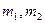 - массы,
- массы,  - скорости до удара,
- скорости до удара, 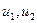 - скорости после удара.
- скорости после удара.
Закон сохранения кинетической энергии:
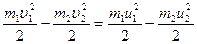 (3.63)
(3.63)
В этом уравнении две неизвестные: 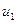 и
и  , поэтому, для того, чтобы задача была решаемой надо привлечь закон сохранения импульса:
, поэтому, для того, чтобы задача была решаемой надо привлечь закон сохранения импульса:
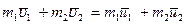 (3.64)
(3.64)
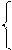 Решим эту систему уравнений:
Решим эту систему уравнений:
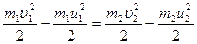
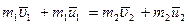
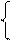
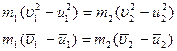
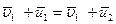 (3.65)
(3.65)
Из (3.65) выражаем  :
: 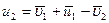
И подставляем закон сохранения импульса:
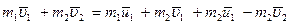
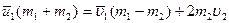
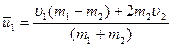 (3.66)
(3.66)
 (3.67)
(3.67)
| <== предыдущая лекция | | | следующая лекция ==> |
| Основная задача динамики. Понятие состояния классической механики. Границы применимости классического способа описания движения частиц | | |
Дата добавления: 2016-04-19; просмотров: 2468;
