Основная задача динамики. Понятие состояния классической механики. Границы применимости классического способа описания движения частиц
Опр.: Динамикой называется часть механики, изучающая динамическое движение, в связи с теми причинами, которые определяют характер движения.
Такими причинами являются взаимодействия между телами.
Основная задача динамики состоит в постановке и поиске решения двух следующих задач:
1. По заданным силам (взаимодействиям) следует установить законы движения тел или точек – прямая задача.
2. По заданным законам движения вычислить силы, действующие на точки или тела – обратная задача.
В классической механике понятия состояния движения частицы в любой момент времени характеризуется положением частицы и величиной скорости. Т.о. необходимо в каждый момент времени точно знать значения координат частицы и ее скорости. При этом образом частицы является геометрическая точка, описывающая с течением времени непрерывную траекторию. Такой способ описания движения частиц имеет принципиальное ограничение.
Согласно квантовой механике, которая обобщает классическую для микромира, невозможно в каждый момент времени знать с одинаковой точностью значения координат частицы и ее скорости. Это вытекает из соотношений неопределенности Гейзенберга, имеющий следующий вид:
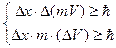 (1.28)
(1.28)
Dx – неопределенность координаты,
DV – неопределенность скорости.
 - постоянная Планка.
- постоянная Планка.

Значение постоянной Планка очень мало, порядок величины составляет 10-34 Дж×с. Поэтому ограничение по классическому описанию частиц актуальны главным образом для микрочастиц, т.е. частиц с очень маленькой массой. В каждом конкретном случае вопрос о том, какое описание приемлемо, классическое или квантовое, решается при помощи исследования данной задачи. Как правило, ограничения на неопределенность какой-либо одной величины бывают известны, тогда из соотношения (1.28) можно вычислить неопределенность второй величины и сравнить полученное значение со значением самой этой величины. Если они одного порядка, то классическим описанием пользоваться нельзя. Если неопределенность гораздо меньше, чем сама величина, то классическим описанием пользоваться можно.
2.1. Первый закон Ньютона. Понятие инерциальной системы отсчета
Если на материальную точку или тело не действуют никакие другие тела или их действие компенсируется, то тело называется свободным.
Движение свободного тела называется движением по инерции.
1 закон Ньютона описывает такое движение. Отметим, что 1 закон Ньютона содержится еще в работах Галилея. Но Ньютону принадлежит только формулировка.
Закон. Всякое тело сохраняет состояние покоя ил равномерного прямолинейного движения, если на него не действуют никакие другие тела или их действие компенсируется.
Следствие. Движение по инерции представляет собой равномерное прямолинейное движение.
 (2.1)
(2.1)
Говоря о равномерном движении или состоянии покоя, необходимо учитывать систему отсчета, относительно которой рассматривается движение.
Т.е. 1 закон Ньютона нельзя формулировать относительно к какой-либо системе отсчета. Возникает вопрос - во всех ли системах отсчета он справедлив. Оказывается не во всех. Есть такие системы отсчета, в которых 1 закон Ньютона справедлив, называющиеся инерциальными системами отсчета (ИСО). Т.о. 1 закон Ньютона из всех возможных систем отсчета выделяет класс инерциальных. Отсюда вытекает другая формулировка 1 закона Ньютона.
Система отсчета – совокупность неподвижных друг относительно друга тел, по отношению к которым рассматривается движение, и отсчитывающих время часов.
1 закон Ньютона называется законом инерции, а инерцией называется свойство тел сохранять величину и направление скорости, когда на него не действуют силы (или действуют уравновешенные силы).
ИСО является система отсчета, начало которой связано с центром Солнца, а оси направлены на неподвижные звезды (называется гелиоцентрической).
2.2. Масса и сила. Эталон массы . Уравнения движения. 2 закон Ньютона как уравнение движения. Сила, как производная импульса
Если попытаться изменить состояние движения какого-либо тела, то тело будет при этом оказывать определенное сопротивление. Это свойство тел называется инертностью.
Количественной характеристикой инертности тела является массы.
Масса – мера инертности тела. Это скалярная физическая величина, которая измеряется в СИ в кг. Обозначается:
[m] =кг.
Для того, чтобы измерить массу какого-либо тела, необходимо эту массу сравнить с массой эталона. Например, рассмотрим взаимодействие двух тел, массами m1 и m2, в результате взаимодействия скорость первого тела изменилась на DV1, а второго на DV1. Эксперименты показывают, что всегда выполняются условия.
 ,
,
 (2.2)
(2.2)
Если вместо m2 взять массу эталона, то по формуле (2.2) можно вычислить массу любого тела. Кроме понятия массы для дальнейшего описания потребуется описание силы.
Силой называется физическая векторная величина, характеризующая взаимодействие тел.
В настоящее время физике известно 4 вида взаимодействия, а именно:
гравитационное
электромагнитное
слабое
сильное
Последние 2 взаимодействия описывают процессы в микромире. Сильное взаимодействие описывает взаимодействие между частицами внутри ядра атома. Слабое описывает процессы взаимного превращения элементарных частиц. Эти взаимодействия являются короткодействующими, проявляются на очень маленьких расстояниях. Оба они не характеризуются понятием силы. Понятие силы характерно для гравитационного и электромагнитного взаимодействий, причем в механике используются не все проявления взаимодействия, а только некоторые:
Силы гравитационного притяжения.
Сила тяжести.
Проявление электромагнитного взаимодействия.
Сила упругости нити.
Сила трения.
Сила упругости деформированного тела.
Сила реакции опоры.
1. Сила трения. Трение подразделяют на внешнее и внутреннее.  .
.
2. Сила упругости. 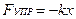
3. Сила гравитационного взаимодействия.  .
.
Для того, чтобы решить основную задачу механики, обычно приходится решать (интегрировать) уравнения движения, имеющие следующий вид:
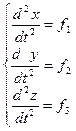 (2.3)
(2.3)
или  (2.4)
(2.4)
Функции f1, f2, f3, f4 определяются характером взаимодействия тел и могут зависеть от координат и времени. Для того, чтобы понять откуда эти функции берутся, сформулируем 2 закон Ньютона. Существует несколько формулировок. Простейшая формулировка:
Закон. Когда на тело действует одна сила и масса тела не меняется, то ускорение, с которым движется тело, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе.
 (2.5)
(2.5)
Если учесть, что ускорение вторая производная от пути, то
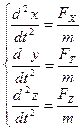 (2.6)
(2.6)
Т.о. 2 закон Ньютона представляет собой уравнение движения тела.
Более сложный случай возникает, если на тело действует несколько сил. Тогда 2 закон Ньютона имеет следующую формулировку:
Закон. Ускорение, с которым движется тело, прямо пропорционально равнодействующей всех сил и обратно пропорционально массе этого тела.
Под равнодействующей мы понимаем сумму всех сил.
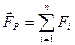 (2.7)
(2.7)
 (2.8)
(2.8)
Из формулы 2 закона Ньютона получается размерность силы:
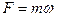 ,
, 
Еще более общий случай 2 закона Ньютона возникает, когда необходимо учесть возможность изменения массы тела.
Для того, чтобы сформулировать 2 закон Ньютона введем понятие импульса тела (количества движения) – это физическая векторная величина, численно равная произведению массы тела на скорость и направленная в сторону движения тела. Обозначается:
 (2.9)
(2.9)
Формулировка 2 закона Ньютона имеет вид:
Закон. Скорость изменения импульса тела равна равнодействующей всех сил, действующих на это тело.
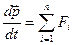 (2.10)
(2.10)
Если (2.9) подставить в (2.10), то формула приобретет следующий вид:
 (2.11)
(2.11)
Если m постоянна,, то ее можно вынести за знак производной.
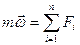 (2.12)
(2.12)
Это означает, что последняя формулировка 2 закона Ньютона является самой общей. Из нее следует другие частные случаи кроме того из этой формулировки понятие силы можно рассматривать, как просто обозначение производной по времени от импульса тела.
Это говорит о том, что сила с такой точки зрения является искусственной характеристикой, то есть можно было бы построить динамику не используя понятия сила.
Но в силу исторических традиций и потому что понятие силы достаточно удобно в динамике это понятие широко используется.
2.3. Законы Ньютона и закон сохранения импульсов
Закон Ньютона описывает взаимодействие двух тел между собой.
Он гласит: «Любые два тела взаимодействуют друг с другом с силами равными по величине, противоположными по направлению и приложены к различным телам».
Математически формулировка закона записывается
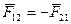
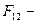 сила, с которой первое тело действует на второе.
сила, с которой первое тело действует на второе.
 сила, с которой второе тело действует на первое.
сила, с которой второе тело действует на первое.
При этом эти силы приложены  ко второму телу, а
ко второму телу, а  к первому телу.
к первому телу.
Поэтому их нельзя складывать и понятие равнодействующей этих сил не имеет смысла.
Отметим, что все три закона Ньютона, справедливы только в инерциальной системе отсчета.
Рассмотрим систему состоящую из нескольких тел, причем тела этой системы взаимодействуют только между собой – такая система тел называется ЗАМКНУТОЙ.
Эксперименты показывают, что суммарный импульс движения тел с течением времени не изменяется – ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
Математически закон сохранения импульса:
 (2.12)
(2.12)
соотношение (2.12) можно получить при помощи второго и третьего закона Ньютона, если учесть, что суммарный импульс замкнутой системы находится как векторная сумма импульсов тел составляющих систему.
Рассмотрим систему состоящую из N-частиц (материальных точек). Обозначим через 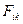 силу, с которой k-я частица действует на
силу, с которой k-я частица действует на
i-ю . 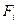 - результирующая всех внешних сил, действующих на i-ю частицу.
- результирующая всех внешних сил, действующих на i-ю частицу.
Уравнения движения всех N- частиц:
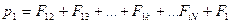
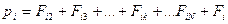



Сложим все уравнения, получится:
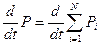
производная по времени.
Сумму внутренних сил можно представить в виде:

Согласно третьему закону Ньютона каждая из скобок =0 следовательно сумма внутренних сил, действующих на тела системы, всегда =0.
 , с учетом этого получим
, с учетом этого получим
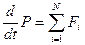 , таким образом производная по времени от суммарного импульса системы равна сумме внешних сил действующих на тела системы.
, таким образом производная по времени от суммарного импульса системы равна сумме внешних сил действующих на тела системы.
Если система замкнута, внешние силы отсутствуют и правая часть уравнения равна нулю. Соответственно  , следовательно p=const.
, следовательно p=const.
Рассмотрим применение закона сохранения импульса к так называемому неупругому удару.
Абсолютно неупругий удар- это такое взаимодействие тел, в результате которого тела движущиеся до взаимодействия раздельно движутся как одно целое.
Обозначим  и
и 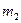 - массы тел,
- массы тел,  и
и  - скорости тел до соударения,
- скорости тел до соударения,  - скорость тел после соударения, тогда импульс системы этх двух тел равен:
- скорость тел после соударения, тогда импульс системы этх двух тел равен:
до соударения  (2.13)
(2.13)
после соударения 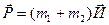 (2.14)
(2.14)
по закону сохранения импульса:
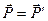 (2.15)
(2.15)
Подставим (2.13) и (2.14) в (2.15), получим:
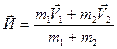 (2.16)
(2.16)
Отметим, что соотношение (2.16) это векторное соотношение, то есть в нем содержится три скалярных соотношения:
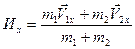 и т. д.
и т. д.
Одно из основных свойств массы, это то, что масса величина аддитивная (суммарная) это значит, что массу любого тела можно вычислить, как сумму масс частей составляющих это тело.
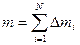 (2.17)
(2.17)
Такое разбиение бывает очень нужным в самых разнообразных случаях, один из них введение понятия центра масс.
По определению это точка, в которой сосредоточена масса всего тела (в котором можно считать сосредот.)
Для введения этого понятия тело мысленно разбивают на материальные точки, к каждой проводят r-вектор, а затем вычисляют r- вектор центра масс по формуле:
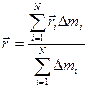 (2.18)
(2.18)
Выясним, что означают слова « в этой точке сосредоточенна масса всего тела». Это значит, что если к телу приложено множество сил к разным его точкам, то в результате, тело движется таким образом как будто к нему приложена одна сила, равная равнодействующей этих сил, причем эта сила приложена к центру масс (инерции) это утверждение называется ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС.
Докажем ее. Для этого, для каждой материальной точки запишем второй закон Ньютона:
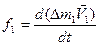
 (2.19)
(2.19)
………………

Суммируем уравнения из системы (2.19)
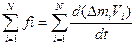 (2.20)
(2.20)
Учтем, что скорость  (2.21) будем считать, что масса каждой материальной точки
(2.21) будем считать, что масса каждой материальной точки  есть величина постоянная, тогда соотношение (2.20) можно переписать следующим образом.
есть величина постоянная, тогда соотношение (2.20) можно переписать следующим образом.
 (2.22)
(2.22)
Меняя местами операции суммирования и дифференцирования:
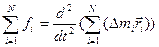 (2.23)
(2.23)
Выражение правой части под знаком суммы это числитель формулы r- вектора для центра масс. Поэтому можно формулу (2.23) преобразуем следующим образом. Умножить и разделить выражение под знаком производной на то выражение, которое стоит в знаменателе для r- вектора центра масс.

Теперь под знаком второй производной находится r- вектор центра масс.
 (2.24)
(2.24)
В левой части (2.24) находится равнодействующая всех сил действующих на тело. В правой части произведение всей массы тала на ускорение точки центра масс (инерции).

точка с – обозначает центр масс тела ч.т.д. Во многих задачах бывает удобно проводить решения в такой системе отсчета, в которой центр масс (инерции) покоится, называется система центра инерции (СЦИ).
2.4. Неинерциальные системы отсчета. Сила инертности
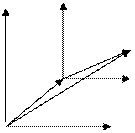
В неинерциальной системе отсчета (НИСО), движущейся по отношению к инерциальным системам с ускорением тело будет иметь ускорение а, отличное от нуля. Поскольку в ИСО F=0, равенство F=ma не соблюдается. Система к является инерциальной. Показанные r – векторы связаны соотношением 
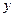

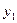
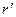 m
m
0 

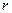
0 
Двухкратное дифференцирование этого соотношения по времени приводит к
 то есть
то есть 
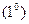
В случае , когда система 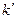 движется поступательно относительно к (то есть
движется поступательно относительно к (то есть 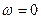 ),
), 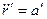 и соотношение
и соотношение 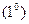 можно переписать
можно переписать  ;
; 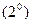
а- ускорение частицы в системе 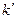 по отношению к системе к.
по отношению к системе к.
Умножим равенство 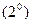 на массу частицы m, и согласно второму закону Ньютона произведение ma дает силу F, поэтому
на массу частицы m, и согласно второму закону Ньютона произведение ma дает силу F, поэтому
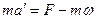

Таким образом, относительно системы 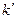 , частица ведет себя так, как если бы, кроме «реальной» силы F , на нее действовала дополнительная «фиктивная» сила
, частица ведет себя так, как если бы, кроме «реальной» силы F , на нее действовала дополнительная «фиктивная» сила 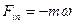 . Эта сила называется СИЛОЙ ИНЕРТНОСТИ. Сила инертности обусловлена свойствами той системы отсчета, в которой рассматриваются мех. явления.
. Эта сила называется СИЛОЙ ИНЕРТНОСТИ. Сила инертности обусловлена свойствами той системы отсчета, в которой рассматриваются мех. явления.
Использовав обозначение силы инертности, напишем уравнение 

2.5. Момент силы и момент импульса. Уравнения движения и равновесия твердого тела (уравнеие моментов)
Важные законы динамики твердого тела связаны с положением момента силы. Существуют два различных понятия: момент силы, относительно точки, момент силы, относительно оси.
1. Пусть О некоторая точка, относительно которой вводится момент силы  . Обозначим
. Обозначим 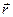 ,
, 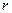 -вектор проведенный из точки О к точки приложения силы F. Тогда моментом силы обозн. Буква М, будет называться физ. Векторная величина, равная векторному произведению
-вектор проведенный из точки О к точки приложения силы F. Тогда моментом силы обозн. Буква М, будет называться физ. Векторная величина, равная векторному произведению 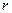 - вектора
- вектора 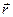 на силу F.
на силу F.
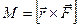 (2.26)
(2.26)





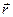
то есть направление моиента силы, находится по правилу векторного произведения, то есть все три вектора взаимно перпендикулярны. Мы ввели понятие момент силы, относительно точки О.
2. Моментом силы относительно оси проходящей через точку О, будет называться проекция момента силы относительно точки на эту ось , таким образом момент силы относительно точки это векторная величина и первичное понятие, а момент силы относительно оси величина скалярная и вторичное понятие.
Если через точку О проходит оси координат, то проекциями момента силы будут  .
.
Они будут моментами силы относительно этих осей. В том случае когда необходимо находить момент нескольких сил относительно точки можно просто векторно сложить момент исходных сил. В том случае, когда линии действия сил лежат в одной плоскости, то момент этих сил относительно этой точки будет равен моменту равнодействующей этих сил относительно точки. Аналогично вводится понятие момента импульса относительно точки и момент импульса относительно оси.


 (2.27)
(2.27)


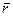
Пусть имеется материальная точка обладающая импульсом р, тогда моментом импульса относительно некоторой точки О, будет физическая величина равная векторному произведению 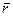 - вектора на импульс
- вектора на импульс  .
.
Моментом импульса относительно оси будет проекция вектора момента импульса относительно точки на ось проходящую через эту точку. Получим уравнение моментов для одной материальной точки. Для этого продифференцируем по времени соотношение (2.27)
 (2.28)
(2.28)
 (2.29)
(2.29)
 (2.30)
(2.30)
 (2.31)
(2.31)
Подставляя эти уравнения в (2.28)
уравнение моментов 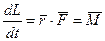 (2.32)
(2.32)
Где мы учли, что 
Уравнение связывает между собой момент силы действующей на материальную точку и скорость изменения момента импульса. Нетрудно увидеть, что формулы (2.31) и (2.32) очень похожи. (2.31) выражает второй закон Ньютона, поэтому можно утверждать, что (2.32) тоже выражает второй закон Ньютона, записанный для моментов, то есть для вращательного движения. Если на твердое тело или точку внешние силы не действуют, или действуют таким образом, что их суммарный момент равен нулю, то тело или точка будут находиться в состоянии равновесия. Таким образом для тела или точки способных вращаться относительно некоторой точки или оси, уравнение равновесия будут иметь вид:
 (2.34)
(2.34)
2.6. Момент инерции тела относительно оси
Рассмотрим простейший случай вращательного движения твердого тела, а именно, когда имеется одна ось вращения ОО и тело вращается вокруг этой оси. В этом случае все точки тела движутся по окружностям, центры которой лежат на оси вращения, а радиусами окружности является расстояние от оси вращения до данной точки.


 |
В этом случае моментом импульса относительно оси ОО, будет проекция момента импульса относительно любой точки лежащей на оси вращения на эту ось. Величина момента импульса относительно оси будет находиться:
L=r*p (2.34)
Такую формулу можно записать для любой материальной точки данного тела если масса материальной точки  , то
, то
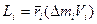 скалярная формула (2.35)
скалярная формула (2.35)
В данном случае 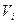 представляет собой линейную скорость точки
представляет собой линейную скорость точки  , движущейся по окружности радиусом
, движущейся по окружности радиусом 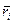 .
.
Если свести угловую скорость 
 (2.36)
(2.36)

Подставим (2.36) в (2.35) получим
 (2.37)
(2.37)
Введем новую физическую величину момент инерции (J) для материальной точки эта величина находится по формуле:
 (2.38)
(2.38)
С учетом (2.38) выражение для момента импульса
 (2.39)
(2.39)
Если просуммировать соотношение (2.39) по всем индексам i, то получим:
 (2.40)
(2.40)
В левой части (2.40) находится момент импульса всего тела, а в правой части произведение угловой скорости на момент инерции всего тела:
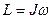 (2.41)
(2.41)
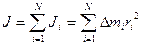 (2.42)
(2.42)
Формула (2.42) выражает значение момента инерции для любого мела, в общем случае эта формула приближенная, и она будет тем точнее, чем на более мелкие части мы разбиваем тело.
В пределе при  мы получим
мы получим
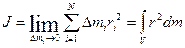 (2.43)
(2.43)
В данном случае интегрирование ведется по всему объему тела, что и отражено значком V , стоящему у интеграла.
Если ввести понятие плотности, то


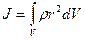 (2.44)
(2.44)
Рассмотрим, как находятся моменты инерции некоторых тел простых конфигураций.
Вывод для стержня, шара, диска.
Сплошной цилиндр (диск) 
Шар 
Прямой тонкий стержень 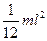 ось перпендикулярна стержню и проходит через середину.
ось перпендикулярна стержню и проходит через середину.
Стержень, ось перпендикулярна к стержню и проходит через его конец 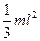
Сфера, ось проходит через центр  .
.
Установим законы механики, связывающие величины, характеризующие вращательное движение.
Пусть потенциальная энергия тела остается неизменной  и изменяется только кинетическая энергия вращательного движения
и изменяется только кинетическая энергия вращательного движения  .
.
В соответствии с определение работы имеем:

так как 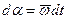 ,то следовательно
,то следовательно

Из этого выражения легко получается закон:

который похож на второй закон Ньютона. Он называется ОСНОВНЫМ ЗАКОНОМ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ:
момент силы, действующий на тело, есть величина, численно равная произведению момента инерции тела на его угловое ускорение.
Как и во втором законе Ньютона, можно учесть зависимость момента инерции тела от времени, и запишем в виде:

2.7. Вращательный момент и момент импульса основной закон динамики вращательного движения
Т.о. момент инерции зависит от:
1. массы тела
2. геометрической формы тела
3. расп-ние масс
4. от положения оси вращения.
Последнее обстоятельство учитывается при помощи теоремы Штейнера.
Момент инерции относительно произвольной оси равен сумме момента инерции относительно оси проходящей через центр масс параллельно данной и произведению массы тела на квадрат расстояния между осями.

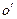
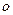

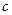
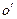
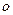

Доказать теорему самостоятельно, расстояние между а равно радиусу цилиндра r. Следовательно для однородного цилиндра:
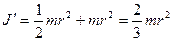
Стержень можно считать тонким, если max поперечный размер его много меньше длины l, следовательно

С помощью этой теоремы можно найти момент инерции 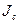 стержня относительно перпендикулярно к нему оси, проходящий через его центр.
стержня относительно перпендикулярно к нему оси, проходящий через его центр.

откуда  для стержня
для стержня
Формула Штейнера
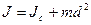
Доказательство теоремы:
Момент инерции J относительно оси О определяется выражением

Разобьем это выражение на три суммы:

Первая сумма представляет собой момент инерции 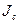 относительно оси, проходящей через центр масс. Сумма
относительно оси, проходящей через центр масс. Сумма  дает массу тела m. И сумма
дает массу тела m. И сумма  , где
, где 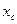 -координата центра масс, которая при сделанном выборе начала координат =0. Т.о. приходим к соотношению:
-координата центра масс, которая при сделанном выборе начала координат =0. Т.о. приходим к соотношению:
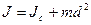
| <== предыдущая лекция | | | следующая лекция ==> |
| Пробій p-n переходу | | | Закон сохранения импульса как фундаментальный закон природы. Реактивное движение |
Дата добавления: 2016-04-19; просмотров: 7169;
