Консервативные и неконсервативные силы. Потенциальная энергия.

Среди всех сил используемых в механике выделяется особый класс сил так называемые консервативные силы.

Это силы, работа которых не зависит от формы траектории по которой перемещается тело, а зависит только от начального и конечного положения тела.

Рассмотрим, например, работу силы тяжести:

Пусть тело массой 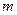, перемещается из · 1 в · 2, под действием силы тяжести.

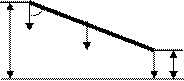В каждой · сила тяжести направлена вертикально. 1

h₁ 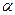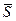2

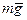
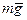
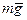h₂

Тогда работа силы тяжести может быть найдена по формуле:

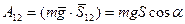(3.55)

Будем считать, что ·1 находится на некоторой высоте h₁, а ·2 - h₂ от произвольного нулевого уровня.

Тогда формула (3.55) принимает вид:

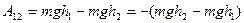(3.56)

Формула (3.56) означает, что работа силы тяжести равна уменьшению некоторой новой величины, которая называется ПАОТЕНЦИАЛЬНОЙ ЭНЕРГИЕЙ.

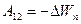(3.57)

Потенциальная энергия силы тяжести:

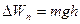(3.58)

Таким образом, сила тяжести - это консервативная сила, которая обладает потенциальной энергией.

Если ввести ось z, направленную вертикально вверх, то можно показать, что:

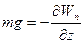(3.59)

На этом примере получены формулы, справедливые для всех консервативных сил, т. е. работа любой консервативной силы F будет равна убыли (уменьшению) потенциальной энергии, которой обладает тело, благодаря действию на него данной силы.

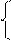
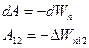(3.60)

Кроме того, если потенциальная энергия зависит от координат x, y, z, то можно записать формулы:

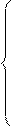
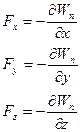(3.61)

которые выражают проекции силы.

Вывести формулы для 2х потенциальных энергий:

1) гравитационного притяжения 2х ·.

2) силы упругости?

1) Когда 1я частица неподвижна и находится в начале координат, можно записать:

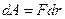F - центральная сила, действующая на эту частицу.

r - радиус вектор этой точки.

А - работа внешних сил.

Если частица притягивается к силовому центру, работа на произвольном пути от ·1 до ·2, определяется выражением:

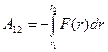
приняв эту работу убыли потенциальной энергии:

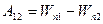
получим: 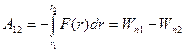(1⁰)

в случае гравитационного притяжения частиц

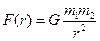
получаем: 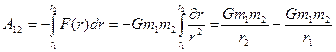(2⁰)

Сопоставление (1⁰) и (2⁰) дает для потенциальной энергии гравитационного взаимодействия 2х частиц выражение:

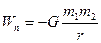
2) Установить, что как для растяжения, так и для сжатия пружины на величину х нужно совершить работу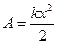

эта работа идет на приращение потенциальной энергии пружины от удлинения х, и имеет вид: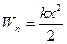

Если в результате действия консервативной силы, тело возвращается в исходную ·, т. е. работа совершается по замкнутому контуру, ясно, что такая работа будет равна нулю:

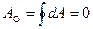(3.62)

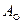- работа по замкнутому контуру.

Соотношение (3.62) также является критерием того, что силы совершающие работу А - консервативны.

Все остальные силы, которые не являются консервативными, являются неконсервативными.

Примеры неконсервативных сил:

1) диссипативные (рассеянные);

2) силы трения или сопротивления.