Основы матричных методов расчета электрических цепей

Лекция N 10

Рассмотренные методы расчета электрических цепей – непосредственно по законам Кирхгофа, методы контурных токов и узловых потенциалов – позволяют принципиально рассчитать любую схему. Однако их применение без использования введенных ранее топологических матриц рационально для относительно 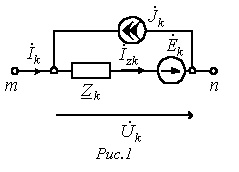простых схем. Использование матричных методов расчета позволяет формализовать процесс составления уравнений электромагнитного баланса цепи, а также упорядочить ввод данных в ЭВМ, что особенно существенно при расчете сложных разветвленных схем.

Переходя к матричным методам расчета цепей, запишем закон Ома в матричной форме.

Пусть имеем схему по рис. 1, где - источник тока. В соответствии с рассмотренным нами ранее законом Ома для участка цепи с ЭДС для данной схемы можно записать:

.

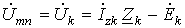(1)

Однако, для дальнейших выкладок будет удобнеепредставить ток 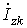как сумму токов k-й ветви и источника тока, т.е.:

.

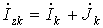(2)

Подставив (2) в (1), получим:

.

(3)

Формула (3) представляет собой аналитическое выражение закона Ома для участка цепи с источниками ЭДС и тока (обобщенной ветви).

Соотношение (3) запишем для всех n ветвей схемы в виде матричного равенства

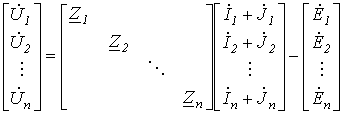
или

,

(4)

где Z – диагональная квадратная (размерностью n x n) матрица сопротивлений ветвей, все элементы которой (взаимную индуктивность не учитываем), за исключением элементов главной диагонали, равны нулю.

Соотношение (4) представляет собой матричную запись закона Ома.

Если обе части равенства (4) умножить слева на контурную матрицу В и учесть второй закон Кирхгофа, согласно которому

,

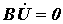(5)

то

,

(6)

то есть получили новую запись в матричной форме второго закона Кирхгофа.