Скважинные системы координат, уравнения траекторий и их погрешности.

В качестве основной системы координат, в которой задается траектория скважины (трубопровода), обычно принимается географическая система координат oNEh (рис.1)с началом в устье скважины и осями расположенными соответственно на север, восток и по вертикали места (обычно, вниз).

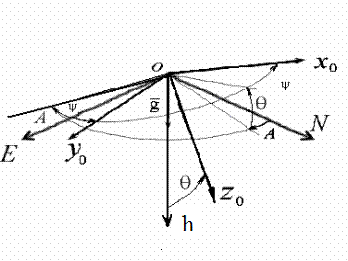
Рис.1

При построении траектории скважины по выходным данным магнитоизмерительных инклинометров может использоваться система координат, связанная с направлением не географического, а магнитного меридиана, в этом случае переход к oNEh осуществляется с помощью известного магнитного склонения.

Задача построения траектории оси ствола скважины (трубопровода) состоит в определении координат его отдельных точек в системе oNEh на основании рассчитанных с помощью инклинометра параметров ориентации оси скважины в соответствующих точках, а также глубины ствола, измеренной по длине колонны труб или геофизического кабеля.

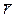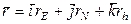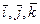Положение касательной к оси скважины в точке измерений, которое в первом приближении можно считать совпадающим с направлением продольной оси СП инклинометра, может быть охарактеризовано единичным вектором : , где - единичные векторы, направленные вдоль осей oN, oE, oh соответственно.

Для определения ориентации вектора 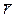вводится связанная с корпусом СП система координат 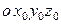, оси которой ориентированы следующим образом: ось 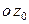расположена вдоль продольной оси СП, а оси 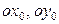лежат в плоскости его поперечного сечения и образуют правый ортогональный трехгранник (рис.1). Плоскость, проходящую через ось 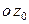и вектор 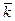, в инклинометрии называют апсидальной.

В общем случае понятие ориентации связано с вращательным движением твердых тел, а задача определения ориентации сводится к нахождению некоторых параметров, которые однозначно задают жестко связанную с твердым телом ортогональную систему координат по отношению к некоторой, заранее заданной или выбранной.

В инклинометрии в качестве параметров ориентации традиционно применяются углы Эйлера, при использовании которых положение связанной с СП системы координат 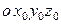относительно географического трехгранника oNEh задается тремя углами: азимутом 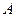, зенитным углом 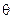и углом 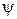поворота корпуса СП вокруг оси 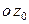(рис. 1).

Азимут 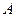- это угол между плоскостью географического меридиана в точке измерения и апсидальной плоскостью. Зенитный угол 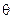- угол между осью 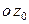и вектором 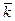. Угол поворота корпуса СП 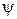- это угол между главной полуплоскостью инклинометра, проходящей через ос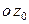и и 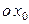, и апсидальной плоскостью. Приняты и другие названия для угла 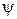: визирный угол, угол установки отклонителя. Последнее название связано с тем, что инклинометр или телеметрическая система контролируют направление действия отклонителя. Углом установки отклонителя 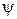называется угол между апсидальной плоскостью и плоскостью действия отклонителя. В дальнейшем будем считать термины угол поворота корпуса СП и угол установки отклонителя тождественными и использовать последний.

В ряде случаев, наиболее адаптированными к построению траекторий скважин (например, близких к вертикальным, как будет показано в дальнейшем) являются не углы Эйлера, а направляющие косинусы.

Матрица направляющих косинусов 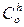, характеризующих ориентацию oNEh (h) относительно трехгранника 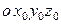(0), определяется следующим образом:

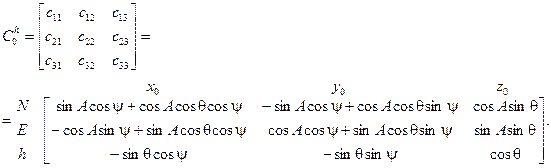(1)

Связь прямоугольных и сферических координат вектора 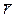может быть представлена в виде:

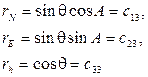(2)

Для построения пространственной траектории оси скважины по результатам инклинометрической съемки разработано и исследовано достаточно большое число методов [ ], которые отличаются друг от друга по сложности реализации и достигаемой точности. Сущность всех методов сводится к выбору той или иной функции для аппроксимации исследуемого интервала искривленного ствола скважины. Как правило, для этого используются один или несколько прямолинейных отрезков, дуга окружности или несколько дуг, а также комбинация дуг и отрезков прямых.

Описание и анализ эффективности всех существующих методов выходит за рамки настоящей работы, однако остановимся на некоторых из них, являющихся самыми распространенными в отечественной промыслово-геофизической практике: тангенциальном, балансном тангенциальном и усреднения углов.

В тангенциальном методе приращения координат на исследуемом интервале ствола 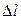определяются по значениям зенитного угла и азимута, измеренным в нижней точке интервала 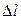, либо по значениям столбца направляющих косинусов 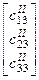в той же точке интервала, следовательно, в этом методе интервал 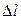аппроксимируется отрезком прямой (см. таблицу 1).

В балансном тангенциальном методе исследуемый интервал 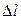разбивается на два участка одинаковой длины: верхний и нижний. Каждый участок аппроксимируется отрезком прямой, причем в качестве исходных данных для построения верхнего и нижнего участков используются значения зенитных углов и азимутов, либо соответствующие значения направляющих косинусов, измеренные соответственно в верхней и нижней точках 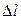. Приращение координат для каждого из участков определяется тангенциальным методом, а результирующие приращения на интервале 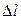находятся как сумма соответствующих приращений на участках (см. таблицу 1).

В методе усреднения углов интервал 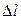между двумя точками замера представляется отрезком прямой, при этом зенитный угол и азимут на протяжении 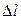принимаются равными средним арифметическим соответствующих углов, измеренных на концах 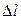(см. таблицу 1). Метод усреднения углов очень прост и в тоже время отличается достаточно высокой точностью. Этот метод является самым востребованным в отечественной практике.

Анализ погрешностей расчета плановых координат скважины указанными выше методами, проведенный многими авторами , показал, что эти погрешности возрастают с увеличением, как шага измерений, так и интенсивности искривления оси ствола в плоскости зенитных углов, при этом наибольшие ошибки присущи тангенциальному методу (рис.1.)

На рис.1. приведены графики зависимости погрешности расчета координат тангенциальным методом от величины шага измерений и интенсивности зенитного искривления, при этом позициям 1,2,3,4 соответствуют следующие значения зенитного угла на забое: 90°, 45°, 15°, 5°.

Рис.1.

Кроме вышеупомянутых методов, иногда используются методы (например, метод расчета по радиусу кривизны (см. таблицу 1)), в которых участок 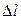аппроксимируется не отрезками прямых, а дугой окружности, проходящей через начало и конец исследуемого интервала. Дуга наилучшим образом соответствует пространственному положению 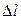, однако и этим методам свойственна возрастающая при увеличении шага измерений и интенсивности искривления ствола погрешность (рис.2).

Рис.2.

На рис. 2. приведены графики зависимости погрешности расчета координат несколькими методами (1 - тангенциальным, 2 - методом усреднения углов, 3 - радиусом кривизны) от величины шага измерений для скважины, имеющей на забое отклонение от вертикали 90°.

При анализе погрешностей определения плановых координат в зависимости от характера искривления оси ствола (с учетом моделей скважин с постоянной, ступенчато-изменяющейся и линейно-изменяющейся интенсивностью искривления ствола одновременно в плоскостях зенитных и азимутальных углов) и применяемом при этом методе вычислений было выявлено [], что для тангенциального метода упомянутые погрешности практически остаются постоянными, для балансного тангенциального метода - могут иметь различные знаки, для метода усреднения углов - возрастают на порядок и более при переходе от постоянной к линейно-изменяющейся интенсивности искривления.

В связи с этим при расчете координат скважин со сложными траекториями в последние годы были разработаны два принципиально новых метода, получивших названия – метод двух хорд и метод трех касательных. Выражения для расчета координат с помощью этих методов приведены в таблице 1.

Метод вычисления координат по двум хордам имеет уровень методических погрешностей практически в 1.5 раза меньше, чем самый применяемый из рассмотренных выше методов (усреднения углов). Еще более точен метод расчета координат по трем касательным – уровень его погрешностей практически на 2-3 порядка меньше, чем при использовании усреднения углов. Метод трех касательных может применяться для расчета координат точек оси ствола с любой, имеющей место в практике бурения, интенсивностью искривления и наиболее востребован в тех задачах, где требования к точности определения координат особенно жесткие (например, при глушении аварийных скважин).

При определении координат соответствующих точек траектории скважины в системе координат oNEh необходимо учитывать то,что сами параметры 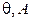или направляющие косинусы 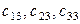, а также длина ствола 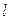, имеют случайные погрешности, которые обычно характеризуются нормальным распределением с нулевыми средними и среднеквадратическими ошибками (СКО) 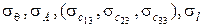соответственно. СКО 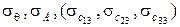могут быть рассчитаны (что будет показано в дальнейших разделах диссертации), если известны модели и численные значения погрешностей чувствительных элементов в составе инклинометров, а также функции их влияния на погрешности определения углов 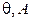или направляющих косинусов .

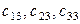Из-за наличия ошибок 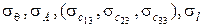координаты точек оси ствола скважины будут определяться также с ошибками 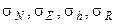, (где ).

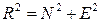Таблица 1 Методы расчета координат	Приращение северной координаты	Приращение восточной координаты	Приращение вертикальной координаты
Тангенциальный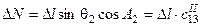
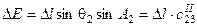
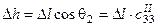
Балансный тангенциальный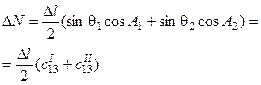
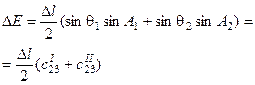
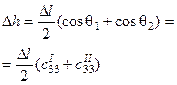
Усреднения углов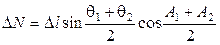
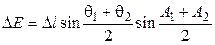
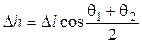
По радиусу кривизны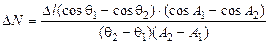
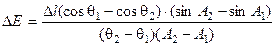
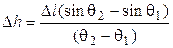
Двух хорд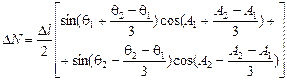
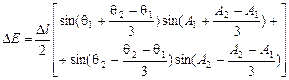
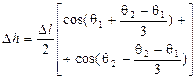
Трех касательных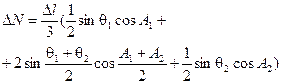

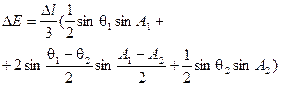
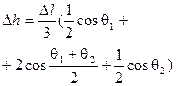
Это вызывает необходимость оценки, так называемых, зон рассеяния координат точек оси ствола (величины неопределенности при расчете каждой координаты). В результате могут быть оценены не только среднее положение оси скважины в пространстве и вероятность попадания забоя в круг допуска, но и доверительная поверхность, внутри которой находится ствол скважины (Рис.3).

Рис.3

Для достоверной оценки погрешностей пространственного положения скважин были разработаны несколько моделей. За рубежом наиболее известна модель Вольфа и де Вардта (так называемая модель WdW), разработанная в 1981г в связи с широким внедрением горизонтального бурения. Эта модель, базируясь на анализе только систематических инструментальных погрешностей существующих в то время магнитных и гироскопических приборов и применяемых методов измерения, представляет собой обобщенную специфическую схему обработки данных эллипса неопределенности пространственного положения скважины, обеспечивающую сведение к минимуму его суммарной погрешности. Модель WdW, претерпевшая более чем за два десятилетия ряд значительных изменений и дополнений, до последних лет оставалась фактически промышленным стандартом. Серьезные ограничения модели WdW и внедрение в производство новых приборов и технологий привели к необходимости замены этой модели.

В настоящее время используются международные промышленные стандарты, использующие модель ISCWSA (модель Industry Steering Committee on Well bore Survey Accuracy, разработанная в 1999году). Эта модель базируется на достаточно полном математическом описании погрешностей чувствительных элементов современных магнитных и гироскопических инклинометров, учитывает как полную, так и неполную компоновку этих элементов, адаптирована к скважинам произвольной ориентации. Модель ISCWSA позволяет выявить и исключить грубые измерения, обеспечивает подтверждение однократных измерений, осуществляет совместную обработку многих измерений с целью минимизации погрешности определения пространственного положения скважин, осуществляет контроль риска столкновений стволов.

Лекция № 7