Трехосные гироинклинометры: компасирование
Алгоритм идеальной работы и погрешности трехосной схемы бесплатформенного гироинклинометра в режиме компасирования
Работа трехосной схемы бесплатформенного гироинклинометра в режиме ГК осуществляются в дискретные моменты времени в условиях неподвижного основания, при этом выходные сигналы трех каналовДУС и линейных акселерометров описываются следующими выражениями:
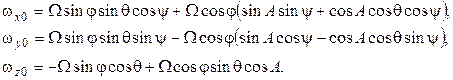 (1)
(1)
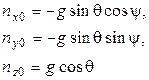 (2)
(2)
где:
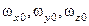 - составляющие вектора
- составляющие вектора 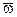 абсолютной угловой скорости вращения трехгранника
абсолютной угловой скорости вращения трехгранника 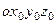 , измеряемые блоком ДУС;
, измеряемые блоком ДУС; 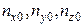 -составляющие ускорения силы тяжести, измеряемые блоком акселерометров;
-составляющие ускорения силы тяжести, измеряемые блоком акселерометров; 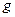 -ускорение силы тяжести;
-ускорение силы тяжести; 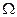 - угловая скорость вращения Земли;
- угловая скорость вращения Земли; 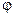 - широта места расположения прибора.
- широта места расположения прибора.
Из выражений (2) можно получить следующие соотношения:
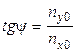 ,
, 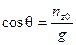 ,
, 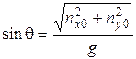 (3)
(3)
и тогда алгоритмы вычисления углов 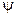 и
и 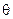 будут иметь вид:
будут иметь вид:
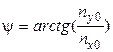 , (4)
, (4)
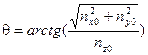 (5)
(5)
Теперь рассмотрим систему трех уравнений (1) относительно оставшегося неизвестным азимутального угла А. Из системы (1) можно получить следующие выражения для тригонометрических функций 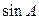 и
и 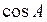 :
:
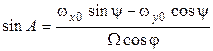 , (6)
, (6)
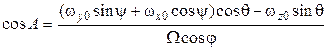 (7)
(7)
При этом значение азимута 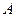 может быть вычислено традиционным образом с применением функции
может быть вычислено традиционным образом с применением функции 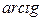 :
:

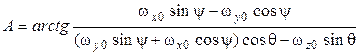 (8)
(8)
Варьирование (8) приводит к следующему выражению для погрешности определения азимута в трехосной схеме:
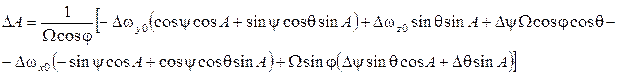
(9)
Вводя кинематические уравнения для погрешностей выработки углов 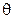 и
и 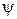 :
:
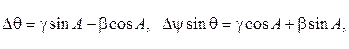 (10)
(10)
где 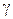 и
и 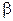 - погрешности моделирования вертикали места [] (
- погрешности моделирования вертикали места [] ( 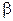 лежит в плоскости меридиана,
лежит в плоскости меридиана, 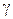 в плоскости первого вертикала), а также вводя переменную
в плоскости первого вертикала), а также вводя переменную 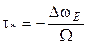 , где
, где
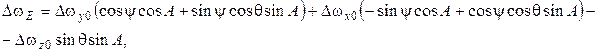 (11)
(11)
получим следующее выражение для погрешности определения азимута:
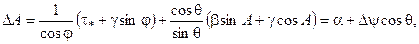 (12)
(12)
где 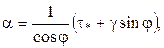 (13)
(13)
- 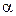 - погрешность моделирования направления полуденной линии, лежащая в плоскости горизонта.
- погрешность моделирования направления полуденной линии, лежащая в плоскости горизонта.
Выражение (13) является известным кинематическим уравнением в теории инерциальных навигационных систем [].
Исходя из выражения (9) и учитывая только погрешности ДУС при условии их статистической независимости и равноточности ( 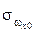 =
= 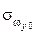 =
= 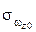 =
= 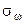 ), можно получить СКО
), можно получить СКО 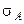 вычисления азимута, которая будет иметь следующий вид:
вычисления азимута, которая будет иметь следующий вид:
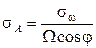 (14)
(14)
Из выражения (14) следует, что СКО определения азимута в трехосной схеме, обусловленная погрешностями ДУС, не зависит от угловых параметров скважины - значений зенитного угла 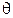 и азимута
и азимута 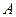 .
.
Алгоритм идеальной работы трехосной схемы бесплатформенного гироинклинометра в режиме БИНС
Алгоритмическую основу непрерывного режима работы трехосной схемы гироинклинометра составляют алгоритмы бесплатформенной инерциальной навигационной системы (БИНС), которые условно можно разделить на алгоритмы выработки параметров ориентации, параметров поступательного движения, а также преобразования кажущихся ускорений, при этом в качестве выходной информации в этом режиме используются только параметры ориентации.
В режиме БИНС матрица направляющих косинусов 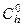 , характеризующая ориентацию связанной с корпусом СП системы координат
, характеризующая ориентацию связанной с корпусом СП системы координат 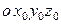 относительно географического трехгранника
относительно географического трехгранника 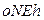 может быть определена интегрированием уравнения Пуассона:
может быть определена интегрированием уравнения Пуассона:
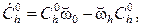 (15)
(15)
где 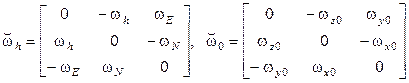 - кососимметрические матрицы, соответствующие векторам угловой скорости вращения географического
- кососимметрические матрицы, соответствующие векторам угловой скорости вращения географического 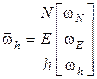 и связанного с корпусом СП
и связанного с корпусом СП 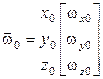 трехгранников.
трехгранников.
Составляющие вектора 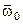 измеряются блоком ДУС.
измеряются блоком ДУС.
Для придания невозмущаемости погрешностей системы линейными ускорениями составляющие вектора 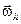 в (15) должны вычисляться по значениям линейной скорости (
в (15) должны вычисляться по значениям линейной скорости ( 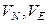 ) и значениям широты места, выработанным в БИНС на основе информации, полученной от акселерометров СП.
) и значениям широты места, выработанным в БИНС на основе информации, полученной от акселерометров СП.
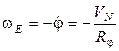 ,
, 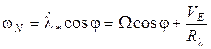 ,
,
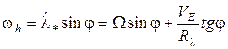 , (16)
, (16)
где 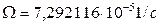 - угловая скорость суточного вращения Земли, а
- угловая скорость суточного вращения Земли, а 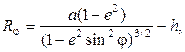
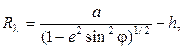 - радиусы кривизны эллипсоида Красовского:
- радиусы кривизны эллипсоида Красовского: 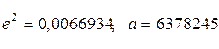 м.
м.
Задача преобразования кажущихся ускорений в бесплатформенном гироинклинометре в режиме БИНС формулируется как задача нахождения проекций 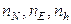 вектора
вектора 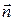 на оси географического трехгранника по информации об измеренных акселерометрами составляющих
на оси географического трехгранника по информации об измеренных акселерометрами составляющих 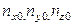 вектора
вектора 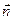 в осях связанного с корпусом СП трехгранника
в осях связанного с корпусом СП трехгранника 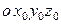 и по вычисленной матрице
и по вычисленной матрице 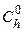 , определяющей взаимную ориентацию трехгранников
, определяющей взаимную ориентацию трехгранников 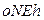 и
и 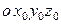 .
.
В блоке выработки параметров поступательного движения осуществляется вычисление составляющих линейной скорости и координат места путем интегрирования составляющих 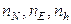 .
.
Исходя из выражения (15) могут быть получены кинематические уравнения углового движения бесплатформенного инклинометра в углах Эйлера:
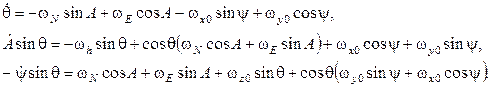 (17)
(17)
Из (15) можно получить соотношения, связывающие угловые скорости вращения трехгранника 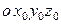 с угловыми скоростями вращения географического трехгранника
с угловыми скоростями вращения географического трехгранника 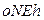 и скоростями изменения углов азимута
и скоростями изменения углов азимута 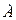 , зенитного угла
, зенитного угла 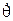 и угла поворота
и угла поворота 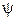 :
:
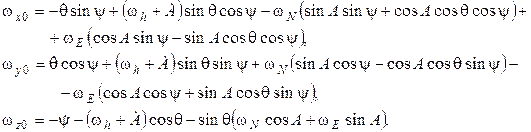 (18)
(18)
Для автокомпенсации инструментальных погрешностей чувствительных элементов в гироинклинометре могут быть предусмотрены модуляционные развороты измерительного блока (ИБ), включающего блок акселерометров и блок гироскопов, вокруг продольной оси СП в диапазоне ±180°. Тогда положение связанной с ИБ системы координат 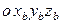 относительно трехгранника
относительно трехгранника 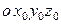 характеризуется матрицей
характеризуется матрицей 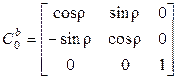 , где
, где 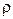 - текущее значение угла разворота вокруг продольной оси СП, которое вычисляется с помощью датчика угла (ДУ), расположенного на этой оси.
- текущее значение угла разворота вокруг продольной оси СП, которое вычисляется с помощью датчика угла (ДУ), расположенного на этой оси.
Матрица направляющих косинусов 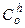 , определяющая ориентацию географического трехгранника
, определяющая ориентацию географического трехгранника 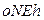 (h) относительно трехгранника
(h) относительно трехгранника 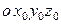 (o), вычисляется как:
(o), вычисляется как:
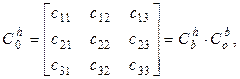 (19)
(19)
где 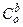 - матрица направляющих косинусов, определяющая ориентацию системы координат
- матрица направляющих косинусов, определяющая ориентацию системы координат 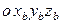 (b) относительно
(b) относительно 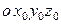 (o).
(o).
Вычисление азимутального, зенитного углов 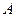 ,
, 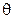 и угла
и угла 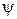 может быть осуществлено по вычисленным элементам матрицы направляющих косинусов
может быть осуществлено по вычисленным элементам матрицы направляющих косинусов 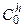 .
.
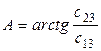 ,
, 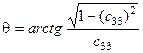 ,
, 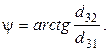 (20)
(20)
Модель погрешностей определения азимута в трехосной схеме гироинклинометра в режиме БИНС
Матрицы 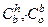 ,
, 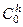 определяются в БИНС с погрешностями, т. е. могут быть определены лишь некоторые оценки
определяются в БИНС с погрешностями, т. е. могут быть определены лишь некоторые оценки 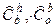 ,
, 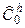 этих матриц, причем
этих матриц, причем
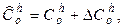
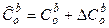 ,
, 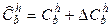 , (21)
, (21)
где 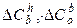 ,
, 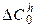 - матрицы, элементы которых определяются варьированием соответствующих матриц
- матрицы, элементы которых определяются варьированием соответствующих матриц 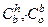 ,
, 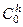 .
.
Подставляя соотношения (21) в алгоритм (19) и, при этом не учитывая величин второго порядка малости относительно рассматриваемых переменных, получим следующее уравнение:
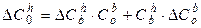 (22)
(22)
Умножая левую и правую части равенства (21) на матрицу 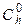 , получим следующее выражение для кососимметрической матрицы погрешностей:
, получим следующее выражение для кососимметрической матрицы погрешностей:
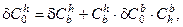 (23)
(23)
и соответствующему ей вектору погрешностей:
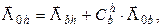 (24)
(24)
которые характеризуют суммарные погрешности гироинклинометра в построении географической системы координат относительно осей корпуса СП.
Составляющие веторов в выражении (24) имеют вид:
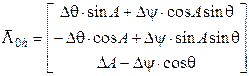 ,
, 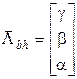 ,
, 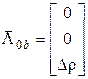 , (25)
, (25)
Если считать, что ДУ измеряет угол 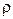 без ошибок (т.е.
без ошибок (т.е. 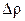 =0) и представить векторное уравнение (24) в скалярной форме, то получим уже известные кинематические соотношения(12) и (13) для погрешностей в выработке параметров ориентации.
=0) и представить векторное уравнение (24) в скалярной форме, то получим уже известные кинематические соотношения(12) и (13) для погрешностей в выработке параметров ориентации.
Воспользовавшись выводом модели погрешнстей БИНС на ДУС, приведенным в , можно получить уже известное кинематическое уравнение, в котором «дрейф восточного гироскопа» 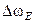 в бесплатформенном гироинклинометре определяется выражением (11).
в бесплатформенном гироинклинометре определяется выражением (11).
Лекция № 8
Дата добавления: 2016-04-14; просмотров: 936;
