Продольная схема гироинклинометра: измерение угловых параметров наклонно-направленных и горизонтальных скважин, особенности построения траекторий скважин.

Если в качестве источника информации об азимуте 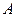рассматривать только выражение (2) (см. лекцию №8), то можно получить следующий алгоритм его вычисления:

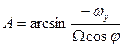(5)

Варьируя (5), получим:

(6)

Как видим, в отличие от (4) «гироскопическая» составляющая ошибки вычисления азимута (5) вообще не зависит от значений зенитного угла, а ее «акселерометрическая» составляющая свободна от зависимости от .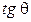

Таким образом, ошибки определения азимута (1) и (5) обладают разными свойствами. Пользуясь этими соотношениями и при этом, учитывая только составляющие, обусловленные погрешностями ДУС, можно определить условие, при котором для вычисления азимута предпочтительней пользоваться алгоритмом (5).

Значения ошибки азимута 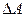, полученные из выражения (4) и (6) обозначим соответственно 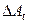и .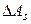

Проверяя условия выполнения неравенства:

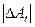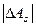< или 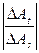< 1, (7)

получим: 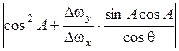< 1, и, далее, используя свойство транзитивности и известное соотношение модуля суммы и суммы модулей, получим: 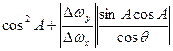< 1. Теперь условие, при котором выполняется 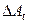< 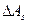, будет иметь вид: <

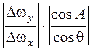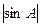
И, наконец, рассматривая (7) применительно к максимально допустимой ошибке и принимая условие равноточности погрешностей ДУС ( ),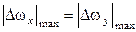

получим: 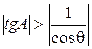(8)

Таким образом, при выполнении условия (8) следует пользоваться для вычисления 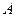алгоритмом (1), в противном случае ─ алгоритмом (5).

Области предпочтительного использования обоих алгоритмов вычисления угла 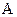наглядно иллюстрируются на картинной плоскости (рис.1). Очевидно, что суммарно эти области гораздо шире, чем области использования традиционного алгоритма, что делает перспективным применение комбинированного алгоритма, предполагающего переключение с одного алгоритма на другой.

Рис.1

В то же время при значении зенитного угла 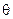= 90° азимут можно вычислить только в соответствии с алгоритмом (5).

Анализ показал, что при пересечении траекторией скважины зоны, граничные значения азимутов которой равны 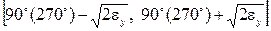(где 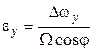), приборное значение перестает меняться. Гироинклинометр оказывается в «мертвой зоне» протяженностью (рис.2, рис.3). Такую же величину имеет диапазон возможных значений, принимаемых (рис.2, рис.3). При попадании в этот «квадрат» и нахождении в нем сверх той протяженности проходки, которая обеспечивает выполнение критерия гладкости:

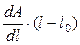< , (9)

где: 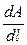─ допустимое искривление скважины ( 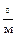); 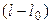─ протяженность проходки на рассматриваемом интервале,

теряется возможность измерения угловых параметров скважины. При выполнении условия (9) выбор между значениями 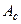и (180°- 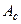) («определение четверти») неоднозначен - выход азимута из «мертвой зоны» становится неконтролируемым, а дальнейшая траектория скважины – ненаблюдаемой и приходится констатировать невозможность решения задач

проводки или контроля скважины гироинклинометром в режиме точечного компасирования.

Рис. 2

Рис.3

Таким образом, подводя итог всему вышесказанному, можно сделать следующие выводы:

1. Для измерения угловых параметров скважин произвольной ориентации с помощью продольной схемы в режиме точечного компасирования следует пользоваться комбинированным, т. е. меняющимся в зависимости от углов ориентации ( 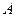, 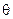) алгоритмом ( 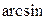или 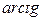), при этом условием «перехода» с одного алгоритма на другой является 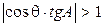. Следует отметить, что область применения алгоритма 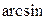гораздо шире, чем 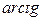, а для горизонтальной скважины с зенитным углом 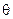= 90° этот алгоритм является единственным, позволяющим вычислить ее азимут.

2.Анализ погрешностей компасирования участков скважин, лежащих в плоскости горизонта и приближающихся к линии «восток - запад» показывает, что и в этом случае сопровождение бурения скважины одногироскопным скважинным прибором возможно, а его погрешности ограничены. Однако, при достаточной протяженности такого участка может произойти потеря наблюдаемости его траектории и, в силу этого, дальнейшая невозможность проводки любого другого горизонтального участка.

Лекция № 10