Произвольной ориентации

Современные разработки непрерывных ГИ, доведенные до реального внедрения, малочисленны и не похожи друг на друга, что предельно облегчает их типизацию. При дальнейшем изложении мы постараемся подойти к их рассмотрению с единых методологических позиций, что, на наш взгляд, упрощает классификацию принципиальных схемноконструктивных и алгоритмических решений.

Схема Z

Из основ теории систем гироскопической ориентации известно, что для вычисления матрицы (1), в общем случае, необходимы три измерителя абсолютной угловой скорости ДУС (три двухстепенных гироскопа или один трехстепенной и один двухстепенной) с осями чувствительности, не лежащими в одной плоскости (в идеале – ортогональными). Однако, при определенных ограничениях на ориентацию скважины и при наличии в составе ГИ акселерометров задача непрерывной съемки может быть решена с помощью только одного трехстепенного, а при ограничениях иного типа – одного двухстепенного гироскопа. Сообразно ориентации осей чувствительности такие схемы ГИ будем обозначать соответственно, XY и Z (рис.1) (см. лекцию № 14) и называть неполными.

Их анализ представляется естественным начать именно со схемы Z потому, что, во-первых, она выглядит наиболее экономичной, а, во-вторых, интуитивно понятно, что областью ее предпочтительного применения должны быть стволы, близкие к вертикальным, по-прежнему преобладающие среди нефтегазовых скважин, особенно подвергаемых повторным измерениям. При этом, еще более очевидной является необходимость измерения в схеме Z значений угловой скорости, определяемых, главным образом, так называемым «моторным эффектом» (крутильными колебаниями геофизического кабеля) и достигающих десятков и даже, если не принять специальных мер по ее ограничению, сотен °/сек.

Приведенные здесь соображения, надо полагать, побудили разработчиков уже упоминавшегося здесь ИГН-73 к созданию его на базе одноосного индикаторного гиростабилизатора (ОИГС) (рис.2). Это оригинальное, даже для девяностых годов, решение, теперь уже можно смело назвать, уникальным, так как более никто по этому пути не пошел.

Технические характеристики ИГН 73 наружный диаметр, мм – 73, длина прибора, мм – 2500; диапазон измерения, град - зенитного угла – 0-70, азимута 0–360.

Основная погрешность определения координаты смещения в плане скважины от пройденного пути:

- не более 0,5% для географической широты ( 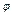) до 60°; не более 0,6% для > 60°, при .

При этом дополнительная погрешность, вызванная изменением - не более 0,1 значения основной на каждые 10° превышения .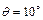

В качестве чувствительных элементов в ГИ ИГН-73 используются двухканальный управляемый гироскоп со сферическим шарикоподшипниковым подвесом типа Д7-03И и два кварцевых акселерометра АТ-1104. Вектор кинетического момента гироскопа ориентирован в плоскости поперечного сечения СП, один канал гироскопа работает в режиме ДУС и используется при начальной азимутальной ориентации платформы гиростабилизатора, другой канал является датчиком системы стабилизации, позволяющей удерживать платформу неподвижной относительно продольной оси СП. Акселерометры, установленные на платформе, измеряют две компоненты кажущегося ускорения.

Рис.2 Схема ОИГС

Матрица ориентации формируется - по информации акселерометров и угловой скорости управления платформой (при бесплатформенной реализации схемы Z эту функцию выполняет информация ДУС с соответствующей осью чувствительности; очевидная аналогия гироплатформы с бесплатформенной схемой позволяет использовать универсальный аппарат для их анализа). Следует подчеркнуть, что, использование ИУ в качестве угломера (маятника), т. е. возможность пренебрежения инерционными ускорениями СП, неоднократно подтверждавшаяся, как оценочными расчетами, так и многолетней практикой является важнейшим, системообразующим фактором скважинной навигации.

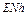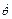Для исследования погрешностей схемы Z воспользуемся одним из уравнений, связывающих абсолютные угловые скорости вращения трехгранника с угловыми скоростями вращения географического трехгранника и скоростями изменения азимута , зенитного угла и угла поворота отклонителя 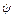(рис.1):

, (7)

где 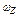- абсолютная угловая скорость вращения трехгранника вокруг оси , измеряемая ДУС; - угловая скорость вращения Земли.

Варьируя уравнение (7) и опуская, с учетом качественного характера проводимого анализа и сравнительно малого времени работы ГИ, составляющие с множителями , получим:

(8)

На основании матрицы (3) можно легко получить выражения для нормированных составляющих ускорения силы тяжести, измеряемых акселерометрами ИУ, варьирование которых приводит к следующим погрешностям :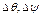

, (9)

где , ,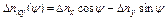

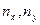- погрешности акселерометров ИУ.

На основании (8) с учетом (9), имеем:

(10)

Далее, полагая погрешности ИУ случайными константами, а угол (для ОИГС) неизменным, получим первые, вполне прогнозируемые, результаты:

- сумму двух первых слагаемых в ви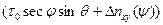де , где - погрешность моделирования оси Мира при компасировании в начальной точке (в ОИГС, определяемая нескомпенсированным дрейфом по оси ДУС); очевидно последнее выражение не имеет особенностей при любых ;

- третье и четвертое слагаемые, определяемые, соответственно, погрешностями акселерометров ИУ и дрейфом по оси стабилизации, стремящиеся к нулю около вертикали ( 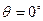) и неограниченно возрастающие по мере приближения к горизонту ( ).

При рассмотрении бесплатформенной реализации схемы Z в дополнение к изложенному следует принять во внимание, что угол поворота отклонителя можно считать меняющимся мало лишь в начале СПО, а при снятии этого ограничения – второе слагаемое (10) приобретает коэффициент при дисперсии погрешности ИУ - , а пятое – с интегралом по - может вообще достичь недопустимых пределов, особенно при малых, быстроменяющихся значений . Ну и, наконец, при использовании в ИУ микромеханических ЧЭ с высоким уровнем флуктуационных погрешностей, весьма значительным, причем, по-прежнему, особенно в зоне малых зенитных углов становится последнее слагаемое в (10).

Тем не менее, настоятельная потребность (речь о которой – ниже) побудила авторов настоящего доклада к практической реализации бесплатформенной схемы Z на MEMS ЧЭ в диапазоне малых зенитных углов. В ходе работы над этой схемой алгоритм (7) был проанализирован и отвергнут, а предложенный «гироазимутальный» оказался свободен от дополнительных погрешностей.

В целях анализа этого алгоритма введем углы и угол (рис. 3).

Рис.3

Показания ИУ могут быть представлены в виде: (11)

а матрица : 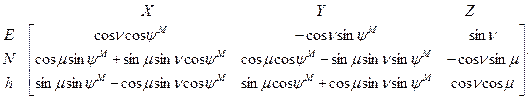(12)

При этом (13)

Понятно, что попытка точного решения системы уравнений (11), (13) наталкивается ровно на те же трудности, что и интегрирование (7). Изменения азимута скважины при малых и отсутствии стабилизации по углу не наблюдаемы. Ситуация, однако, предельно упрощается, если малость и (т. е. в конечном счете ) позволяет пренебречь вторым членом в правой части (13). Варьируя элементы последнего столбца (12) и предполагая (для наглядности) кратковременность прохождения вертикального ствола, разрешим, с учетом малости 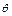, полученную систему уравнений относительно

(14)

«Разгадка» эффективности (а заодно и названия) «гироазимутального» алгоритма полностью исчерпывается последней формулой, из которой следует, что погрешность вносимая упрощением (13) пропорциональна . Локализация бесплатформенной схемы Z вблизи вертикали, таким образом, может быть не слишком жесткой, но, при этом, она позволяет отказаться от необходимости решения уравнений Пуассона и, следовательно, от имитации сигналов угловых скоростей с помощью акселерометров, приемлемой только в ОИГС. О реальных и планируемых применениях рассмотренной схемы и данных ее апробации – см. ниже.

Схема ХY

Этим очевидным, берущим начало в практике точечного компасирования, решением («продольная компоновка» и т.д.) легко парируется основная проблема предыдущей схемы – необходимость измерения большой угловой скорости. В данном случае, диапазон измерения ДУС по осям X и Y определяется величинами 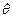и sin 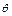, которые, во всяком случае, при обеспечении центрирования прибора в скважине, не превышают значения 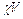≤ 0,5°/сек (здесь 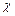- кривизна скважины, °/м; V - линейная скорость СПО, м/сек). С учетом двух-трехкратного запаса, определяемого, прежде всего, неидеальностью центрирования, такой диапазон обеспечивается достаточно точными ДУС, как с механическим носителем вектора кинетического момента, так и без оного.

Хорошо известные алгоритмы схемы XY имеют следующий вид (рис.1):

= ,

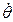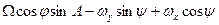= , (15)

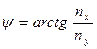, (16) 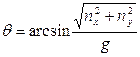(17)

В этих алгоритмах, как и в схеме Z, ИУ выполняет функцию угломера. Точность выработки 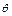может быть повышена за счет комплексирования его значений, полученных из (17) и (15), однако это отличие, не играет первостепенной роли. А вот ошибка определения азимута 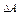, в отличие от (8), неограниченно растет при →0, и, таким образом, область предпочтительного применения схемы Z - для продольной компоновки, как будто бы, оказывается под запретом.

Во всяком случае, этим в течение многих лет руководствовался мировой лидер в области ГИ для непрерывной съемки - Gyrodata , уже упоминавшаяся в I разделе в качестве разработчика RGS-С.

Основные характеристики Rate-gyroscopic system continued (RGS-C): наружный диаметр – 1,75˝ (44,45мм), длина СП – 3000мм; - диапазон измерения, град: зенитного угла – 0-120, азимута - 360°; предельная рабочая температура, °С – 150; предельное давление, МПа – 100. Режим работы изделия в диапазоне зенитных углов – 0°÷15° - точечный; - 15°÷120° - непрерывный, декларируемая точность – 0,1% от глубины по стволу.

Использование точечного компасирования вплоть до 15° по зениту объясняется, видимо, приоритетом точности над производительностью при съемке достаточно протяженных стволов с небольшим отстоянием от вертикали (при , схема XY имеет в непрерывном режиме большие погрешности, чем в точечном). Кроме того, необходимо подчеркнуть принципиальное различие свойств рассматриваемых схем в части касающейся начальных условий. В схеме Z выставка-компасирование (как в ОИГС) или внешняя (как в бесплатформенном варианте) – производится только в устье скважины. В схеме XY выставки (как правило, гирокомпасирования) в устье может оказаться недостаточно – основным условием является, все-таки кратковременность нахождения на участке ствола близ вертикали. С другой стороны компасирование в этой схеме может производиться практически всегда в процессе съемки.

Как бы то не было, ни эти, достаточно прозрачные, соображения, ни, вообще, приоритет анализа ошибок углов ориентации ствола, характерный для времен разработки RGS-C, ни в коей мере не оправдывают исключение возможности непрерывной съемки значительной (а для России, - преобладающей) доли скважин, траектории которых целиком (или в основном) лежат внутри указанного диапазона зенитных углов.

Автор данного конспекта, начиная разработку непрерывного ГИ типа XY, лет на десять позже, чем коллеги из Gyrodata, и всего лишь через три года после обращения к инклинометрической тематике, был свободен от «призраков прошлого» и сделал предметом исследования характеристику промаха в плане . При этом было установлено, что при малых зенитных углах полагать характер поведения , определяемым погрешностью горизонтирования, отнесенной к малой величине , по меньшей мере, неточно. Чтобы убедиться в этом, на качественном уровне, достаточно проварьировать уравнение (15), (пренебрегая членами с и, полагая, cos =1, sin = ), а также (16) и проинтегрировать полученную систему линейных нестационарных дифференциальных уравнений. При этом получим:

(18)

где ,

Сравнивая (18) с (10) нетрудно убедиться, что (для вертикального ствола) к двум первым слагаемым вполне применимы выводы, полученные для бесплатформенной реализации схемы Z. Сравнительно малое время прохождения вертикального ствола, позволяет не принимать во внимание последнее слагаемое, обусловленное уходами гироскопов. Третье слагаемое в (18), в силу, как правило, больших значений при малых , и быстрых изменениях последнего, может в разы превышать уровень инструментальной погрешности ИУ, но, это не меняет главного вывода – какой-либо количественный критерий по углу для ограничения работоспособности схемы XY отсутствует.

Тем не менее, сложности при практическом использовании такого ГИ вблизи вертикали, конечно, возникают, причем основными инструментальными факторами здесь являются шумы акселерометров и конечная частота дискретизации измерительной информации. Весовые функции при этих возмущениях в правой части (18), в общем случае, нестационарны, и от того, насколько существенна эта нестационарность (определяемая, в свою очередь, величиной т.е. отчасти, управляемая), прежде всего, зависит степень влияния флуктуационных погрешностей и малой дискретности.

Рис.4

Рис.5

На рис.4 и рис.5 приведены погрешности выработки плановых координат при съемке скважин гироинклинометром УГИ-42.03, выполненным по схеме XУ. (рис 4 - скважина 304, месторождение Т-Русскинское, куст 13с, «Когалымнефтегеофизика», рис..5 – скважина 1792, месторождение Лянторское, куст 324, «Сургутнефтегаз»). Из рис.4 следует, что, несмотря на то, что среднее значение на первых 130м не превышает 0.6°, ошибки плановых координат находятся глубоко в допуске, что абсолютно согласуется с малостью и . В то же время на рис. 5 уже к 90м ошибка в плане превышает 1%, при том, что поведение на этом участке ствола не менее благоприятно, чем в предыдущем случае. Здесь все объясняется поведением азимута, скорость изменения которого такова, что его определение ГИ сопровождается потерей знака и сбоями на 180°(!). Заметим, что бурное развитие как микропроцессорной, так и микросистемной техники позволяет, конечно, на этапе модернизации изделий серьезно продвинуться и в части повышения быстродействия контроллера, и в части снижения шума акселерометров, что, вероятно, позволит отодвинуть границу применяемости схемы XY к значениям (0,2÷0,25)°. Однако, ограничение универсальности (например, при работе на вертикальных стволах большой протяженности – подземные газохранилища, «правильно» пробуренные скважины старого фонда - с сохранением точностных требований) все равно остается стимулом к поиску более общих решений.

Сравнительные характеристики неполных схем. Результаты испытаний. Перспективы.

Ниже приводятся сравнительные характеристики по основным показателям ГИ (таблица 1).

Однозначные выводы о предпочтительности той или иной схемы, очевидно, были бы затруднительны, если не принимать во внимание возможности их технической реализации. ДУС для создания бесплатформенного варианта схемы Z в «нефтегазовом» сегменте рынка сегодня не существует. Единственная, как уже было сказано, существующая разработка ОИГС обладает негативными особенностями конкретной реализации, обусловленными качеством сухих гироскопических ЧЭ – большой нестабильностью и сложной пространственной моделью дрейфа, что, в свою очередь определяет необходимость частых остановок для его уточнения в процессе съемки, а также длительность и жесткую привязку к вертикальному положению СП процесса начальной выставки. При больших 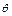нестабильность дрейфа приобретает «коэффициент усиления», равный tg , что, в конечном счете делает использование ГИ невозможным. Возможна модернизация схемы ИГН-73 посредством использования (например, при >45°) информации ДУС, коим является гироскоп ОИГС по оси, перпендикулярной оси стабилизации (см.рис.2). Таким образом, реализуется режим, аналогичный бесплатформенной схеме XY. Этого, однако не происходит, что, по всей видимости, объясняется техническими сложностями при создании нового режима и/или отсутствием при строительстве современных скважин сложного профиля интереса к ГИ с Æ73мм, который определяется использованием, так называемой – поперечной схемы при создании ОИГС.

Таблица 1

Показатель качества	Схема Z	Схема XY
Диапазон измерения угловой скорости	40°/сек и более для бесплатформенного ГИ; либо ОИГС	(1÷2)°/сек
Точность, в зависимости от угла	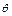Высокая, при →0° Соизмеримая с XY при 35°< <55° Низкая при >70°, при →90 неприменима	Не зависит
Точность на вертикальных ( <(1÷2)°)стволах при большой (>1км) глубине	Высокая	Ниже, чем у Z в раз
Начальная выставка: - автономная   - внешняя	Только для ОИГС на трехстепенном гироскопе Без ограничений	Без ограничений   Только при «быстром» отходе от вертикали

Построение ГИ по схеме XY напротив выглядит просто. Концептуальные задачи, подлежащие решению в процессе его создания – также почти очевидны. Первая из них – применение удароустойчивого ДУС и создание условий, минимизирующих влияние его дрейфов при малых 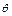(иначе, при равноточных гироскопах в таких стволах схема XY явно уступает схеме Z). Другая задача –минимизация влияния нестационарности алгоритмов идеальной работы (15) и (16) и нелинейности их реализации при →0 .

Однако решения только этих задач может оказаться недостаточно. Поэтому при модернизации, упомянутого инклинометра УГИ-42, основная схема XY была дополнена «бюджетным» вариантом бесплатформенного «гироазимута» с алгоритмами (11) на MEMS гироскопах. Результаты съемки различных скважин с помощью ИГН-73 и УГИ-42.03 представлены на рис.6 (скважина 6146, куст 184, месторождение Тевлино-Русскинское, «Когалымнефтегеофизика») и рис.7 (скважина 3243, куст 144, месторождение Западно-Сургутское, «Сургутнефтегаз»). Понятно, что отсутствие эталонирования в ходе реальной эксплуатации оставляет для анализа точности единственную возможность – оценку по невязке, которая показывает, что съемка с помощью полученного описанным образом комплексного ГИ не менее эффективна, чем с ОИГС, несмотря на ориентацию скважин более предпочтительную для схемы Z. И хотя анализ синтезированной схемы XYz (малость последнего индекса вполне соответствует, как вспомогательной функции MEMS гироскопа, так и «легкости» его введения в ГИ) - не предмет исследования в данной работе, отметим, что ее эффективность всецело определяется апостериорной обработкой – еще одним системообразующим фактором скважинной навигации.

Рис.6 Рис.7

Лекция 16