Оценка называется несмещенной, если ее математическое ожидание

равно истинному значению оцениваемой величины.

В том случае, когда можно найти несколько несмещенных оценок, лучшей из них считается та, которая имеет наименьшую дисперсию. Чем меньше дисперсия оценки,

тем более эффективной считают эту оценку.

Точечной оценкой математического ожидания МО результата измерений является среднее арифметическое значение измеряемой величины

При любом законе распределения оно является состоятельной и несмещенной оценкой, а также наиболее эффективной по критерию наименьших квадратов.

Точечная оценка дисперсии, определяемая по формуле

является несмещенной и состоятельной.

Оценка среднего квадратического отклонения СКО

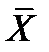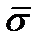Полученные оценки МО и СКО являются случайными величинами. Это проявляется в том, что при повторении несколько раз серий из n наблюдений каждый раз будут получаться различные оценки и . Рассеяние этих оценок целесообразно оценивать СКО S_x . Оценка СКО среднего арифметического значения

Полученные оценки позволяют записать итог измерений в виде

Интервал, определяемый правой частью этого равенства, с некоторой вероятностью «накрывает» истинное значение Q измеряемой величины. Однако точечные оценки ничего не говорят о значении этой вероятности. Рассмотренные точечные оценки параметров распределения дают оценку в виде числа, наиболее близкого к значению неизвестного

параметра. Такие оценки используют только при большом числе измерений. Чем меньше объем выборки, тем легче допустить ошибку при выборе параметра. Способы нахождения оценок результата зависят от вида функции распределения и от имеющихся соглашений по этому вопросу, регламентируемых в рамках законодательной метрологии. Распределения погрешностей результатов наблюдений, как правило, являются симметричными относительно центра распределения, поэтому истинное значение измеряемой величины может быть определено как координата центра рассеивания Xц , т.е. центра симметрии распределения случайной погрешности (при условии, что систематическая погрешность исключена). Отсюда следует принятое в метрологии правило оценивания случайной погрешности в виде интервала, симметричного относительно результата измерения (Xц ± Δx).