Простая модель изображения 3D объекта в виде каркаса.

1). 3D ГСК – СК изображения (ГСК + Z координата)

2). Единица измерения – пиксель.

3). Проекция параллельная.

Для эффекта перспективного укорачивания: преобразование объекта, при котором при параллельной проекции вычисления как при центральной.

x’ = (x*d) / z ,d = 1000п (условное)

y’ = (y*d) / z

z’ = z

Итог.

Получен каркас, но с помощью него можно определить множество различных объектов.

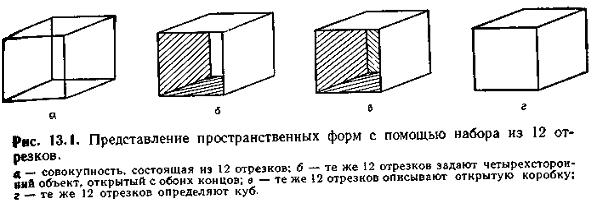
чтобы представить трехмерный объект нужно описать поверхность (стирание невидимых плоскостей, окраска объекта).

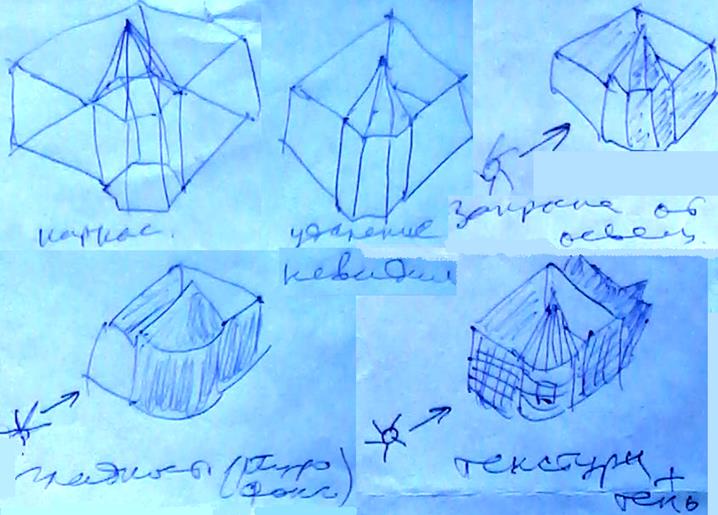
В качестве примера рассмотрим сложное преобразование, заключающееся во вращении на угол 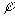вокруг прямой, проходящей через точку T(X, Y, Z) и имеющую направляющий вектор V(l, m, n), причем l²+m²+n²=1, т.е. вектор V является единичным.

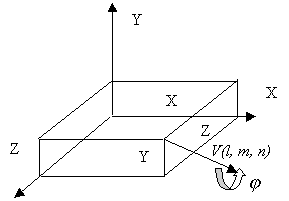Необходимо разложить преобразование на ряд элементарных шагов (базовых преобразований).

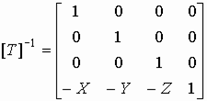Цель: развернем систему координат так, чтобы ось Z совпала с V, после чего поворот на угол 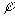будет возможно произвести путем осуществления базового преобразования - поворота на этот угол вокруг оси Z. Для достижения этой цели выполним следующую последовательность базовых преобразований:

1. Перенос вектора V в начало координат:

2. 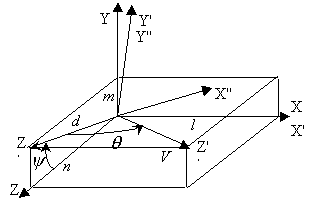Поворот системы координат на угол 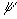вокруг оси X (т.к. разворачиваем "систему координат" по часовой стрелке, то это тоже самое, что разворот точки против часовой стрелки). Чтобы вектор V «лег» на плоскость XoZ

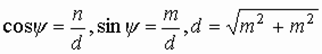
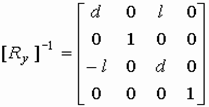
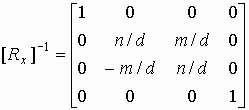
3. 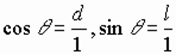Поворот системы координат вокруг оси ординат Y на угол 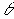чтобы V «лег» на oZ

4. 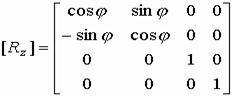Поворот вокруг V на угол 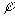, а т.к. V совпадает с осью аппликат Z, то матрица этого преобразования имеет следующий вид:

А так как нам необходимо вернуться в исходную систему координат, то:

5. Поворот вокруг оси ординат на угол " 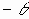" - [R_y]

6. Поворот вокруг оси абсцисс на угол " 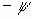" - [R_x]

7. 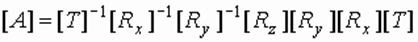Перенос на вектор T(X, Y, Z).

Результирующая матрица имеет следующий вид: