Представление пространственных форм.
Лекции 8. Геометрические основы машинной графики.
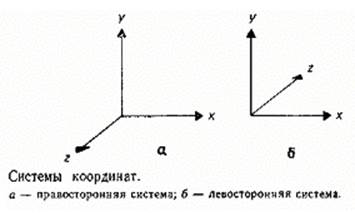 Представление 3-хмерного объекта в ЭВМ.
Представление 3-хмерного объекта в ЭВМ.
Любая непрерывная поверхность – это бесконечное множество точек. Поэтому необходимо взять только некоторые точки, в которых реальный объект соответствует машинному представлению объекта (аппроксимация объекта).
Каждая точка в пространстве описывается координатами, т.е. нужна система координат, в которой задается объект. Выбирают линейную систему координат, обычно декартовую.
М.С.К. –мировая система координат
Н.С.К. –система координат наблюдателя
Л.С.К. (О.С.К.) –локальная (объекта) система координат
1. ОСК -> МСК 2. МСК -> НСК 3. НСК -> ГСК (графическая СК)
Представление пространственных форм.
Область - геометрическое моделирование
2 способа представления трехмерных поверхностей в пространстве: полигональная сетка и параметрические бикубические куски (сплайны).
 Полигональной сеткой является совокупность связанных между собой плоских многоугольников. Наиболее полно представляются объекты правильных прямоугольных форм: здания, мебель и т.д. Можно представить и любые криволинейные формы путем линейной аппроксимации (триангуляция - треугольниками).
Полигональной сеткой является совокупность связанных между собой плоских многоугольников. Наиболее полно представляются объекты правильных прямоугольных форм: здания, мебель и т.д. Можно представить и любые криволинейные формы путем линейной аппроксимации (триангуляция - треугольниками).
Недостатком этого метода является его приблизительность. Чем больше многоугольников в сетке тем больше точность, но и больше требуется памяти и времени на обработку.
Полигональная сетка представляет собой совокупность ребер, вершин и многоугольников. Вершины соединяются ребрами, а многоугольники рассматриваются как последовательности ребер или вершин.
Параметрические бикубические куски описывают координаты точек на искривленной поверхности с помощью трех уравнений (по одному для х, у и z). Каждое из уравнений имеет две переменные (два параметра), причем показатели степени при них не выше третьей (отсюда название бикубический). Границами кусков являются параметрические кубические кривые. Для представления поверхности с заданной точностью требуется значительно меньшее число бикубических кусков, чем при аппроксимации полигональной сеткой. Однако алгоритмы для работы с бикубическими объектами существенно сложнее алгоритмов, имеющих дело с многоугольниками.
При использовании обоих методов трехмерное тело представляется в виде замкнутой поверхности. В отличие от этого при моделировании сплошных тел имеют дело с твердыми объектами. В качестве примитивов выступают такие тела, как кубы, конусы, сферы и цилиндры, которые можно объединять и вычитать, образуя различные формы.
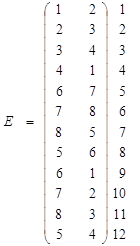
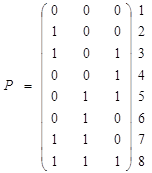 Способы задания многоугольников.
Способы задания многоугольников.
Представление объекта в виде каркаса.
1. Список, матрица вершин P ‑ единичный куб от (0,0,0) вправо-назад, низ против часовой 1234, верх – 6785
2. Список ребер E. Ребро – отрезок прямой, определяется двумя вершинами.
Каркас объекта – это совокупность вершин и ребер объекта. Вершины образуют список или матрицу вершин, ребра – матрицу ребер.
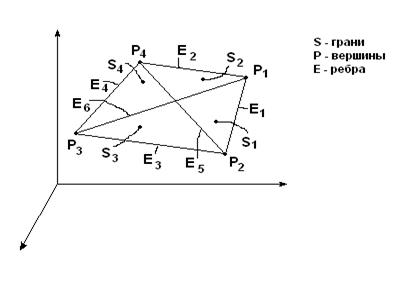 1. Явное задание многоугольников.
1. Явное задание многоугольников.
Каждый многоугольник можно представить в виде списка координат его вершин. Вершины запоминаются в том порядке, в котором они встречаются при обходе вокруг многоугольника. При этом все последовательные, вершины, а также первая и последняя соединяются ребрами. S:
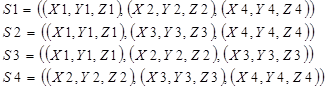
или матрица 4 3 3
Недостатки:
1. Громоздкая матрица.
2. Вершины входят в описание много раз.
3. При выводе каждого многоугольника будут повторяться ребра.
4. Много исправлений при смене одной вершины.
Дата добавления: 2016-04-14; просмотров: 1086;
