Когерентность ребер и алгоритм построчного сканирования.

Первый шаг процедуры, т. е. вычисление пересечений, может оказаться медленным. Каждое ребро многоугольника требуется сравнивать с каждой сканирующей строкой. Во многих случаях лишь небольшое число ребер будет представлять интерес. Более того, необходимо отметить, что многие из ребер, пересекаемых строкой i, будут пересекаться также строкой i+1. Такая когерентность ребер (аналогичная когерентности сканирующих строк, рассмотренной выше) проявляется всякий раз, когда сканирующие строки пересекают ребро. При переходе от одной строки к другой можно вычислить новую x-координату точки пересечения ребра, используя x-координату старой точки пересечения (аналогично случаю развертки отрезков):

где m — тангенс угла наклона ребра. Параметр m равен Dy/Dx, а Dy=1, так что 1/m=Dx;.

Можно воспользоваться когерентностью ребер и устранить лишние сравнения сканирующих строк и ребер путем построчного разложения многоугольника в растр снизу вверх (или сверху вниз), используя алгоритм построчного сканирования.

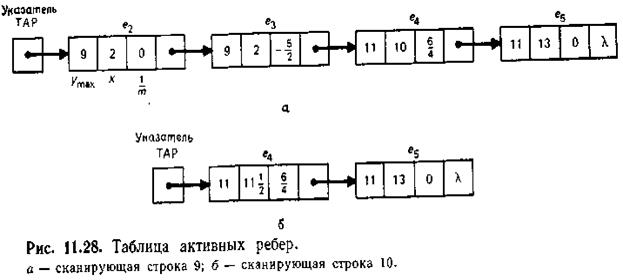
Для каждой сканирующей строки рассматриваются только те ребра, которые пересекают строку. Они задаются таблицей активных ребер (ТАР). При переходе к следующей строке новые значения х-координат точек пересечения вычисляются с помощью уравнения (11.14), все новые ребра, пересекаемые следующей сканирующей строкой, добавляются в ТАР, а те ребра, которые содержатся в ТАР, но не пересекаются со следующей строкой, удаляются. Ребра, содержащиеся в ТАР, упорядочиваются по значениям x-координат точек пересечения, поэтому можно легко находить последовательности пикселей, которые следует закрасить.

Для эффективной реализации включения ребер в ТАР вводится таблица ребер (ТР), которая содержит все ребра, упорядоченные по значениям их меньших y-координат. ТР обычно строят с помощью групповой сортировки, выделяя столько же групп, сколько имеется сканирующих строк. Внутри каждой группы ребра располагаются в порядке возрастания x-координат наиболее низких точек. Этот порядок устанавливается с помощью сортировки вставками. Каждый элемент ТР содержит большую y-координату ребра (y max), x-координату нижней точки (x min) и приращение х, используемое для перехода от одной сканирующей строки к следующей (1/m).

На рис. 11.27 показано, как были бы отсортированы шесть ребер, изображенные на рис. 11.25, в предположении, что соответствующие ребра были предварительно укорочены на одну строку каждое, чтобы избежать двойных пересечений.

На рис. 11.28 приведена ТАР в случае сканирующих строк 9 и 10 для многоугольника, показанного на рис. 11.25.

После того как ТР сформирована, алгоритм построчного сканирования складывается из следующих шагов:

1. Установить у, равным минимальному значению координаты у среди элементов ТР, т. е. совпадающей с у-координатой первой непустой группы.

2. Инициализировать ТАР, сделать ее пустой.

3. Повторять шаг 3 до тех пор, пока ТАР и ТР не станут пустыми:

3.1. Слить информацию из группы у в ТР с информацией в ТАР, сохраняя упорядочение по х-координате.

3.2. Занести желаемые значения в пиксели на сканирующей строке, определяемой текущим значением у, используя пары x-координат из ТАР.

3.3. Удалить из ТАР те элементы, в которых y=ymax

3.4. Для всех элементов, содержащихся в ТАР, заменить х на х+1/m. Тем самым пересечение со следующей сканирующей строкой заносится в каждый элемент ТАР.

3.5. Поскольку на предыдущем шаге могла нарушиться упорядоченность ТАР по х, провести пересортировку ТАР.

3.6. Увеличить у на 1 и, таким образом, перейти к следующей сканирующей строке.

В этом алгоритме для эффективности преобразования многоугольника в растровую форму используются когерентность ребер сканирующих строк, а также сортировка.

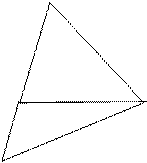
Наиболее просто осуществляется построчная закраска треугольника (в 3D графике треугольник – это основной элемент аппроксимации криволинейных поверхностей):

1.

2. разбиваем на 2 треугольника:
‑ выше средней вершины (1,3,4)
‑ ниже средней вершины (4,3,2)
=> вводится новая псевдовершина (X4,Y4)

3. сортируем среднюю и новую вершины по горизонтали:
‑ левая (X4,Y4)
‑ правая (X3,Y3)

4. строим уравнения прямой для левого и правого ребер:
‑ от (X1,Y1) до (X4,Y4) - левая (идентично (X1,Y1)-(X2,Y2))
‑ от (X1,Y1) до (X3,Y3) - правая
по формуле X=(Y-Yn)*(Xk-Xn)/(Yk-Yn)+Xn

5. построчная закраска треугольника горизонтальными прямыми:
внешний цикл for Y:=Y1 to Y3
внутренний цикл for X:=Xл(Y) to Xп(Y)

6. повторяем 4)-5) для нижнего треугольникаfor Y:=Y3 to Y2

X1,Y1

X4,Y4 X3,Y3

X2,Y2