Лекции 8. Растровая развертка многоугольников.

Объект задан в каркасной форме в ГСК.

В порядке сканирующихся строк экранным лучом определить принадлежность точки многоугольнику и вывести с заданными атрибутами.

Такой процесс неэффективен, поскольку последовательность соседних пикселей обычно принадлежит многоугольнику.

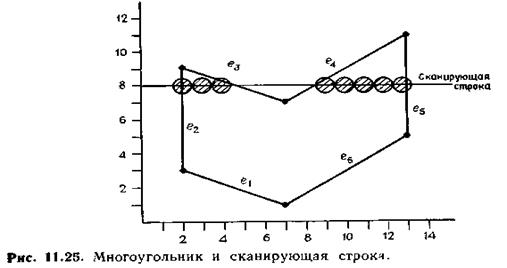
Свойство когерентности растровых строк: соседние пиксели имею один атрибут, смена атрибута происходит на пересечении с ребрами. На сканирующей строке 8 (рис.11.25) внутри многоугольника находятся две полосы пикселей, которые можно закрасить тремя этапами:

1. Найти пересечения сканирующей строки со всеми ребрами многоугольника.

2. Упорядочить точки пересечений по возрастанию координаты х.

3. Раскрасить все пиксели между парами точек пересечения.

Для рис. 11.25 в упорядоченном списке x-координат точек пересечения будут числа (2, 4, 9, 13). Поэтому закрашиваются все пиксели в интервалах 2—4 и 9—13.

Горизонтальные ребра не могут пересекать сканирующие строки и поэтому не рассматриваются.

Пересечения вершин.

Проблема: если число точек пересечения в отсортированном списке нечетно, процедура раскраски работает неправильно. Это возможно, когда сканирующая строка пересекает вершину, в результате чего в список пересечений заносятся две точки пересечения. Рассмотрим, например, строку с у=3 (рис. 11.25). Она пересекается с ребрами многоугольника в точках 2, 2 и 10. Тогда последовательность пикселей от 2 до 2 (т. е. пиксель в точке x=2, у=3) закрасилась бы, совокупность пикселей от 3 до 9 осталась бы незакрашенной, а последовательность от 10 до правой границы буфера закрасится.

Прохождение сканирующей строки через вершину следует считать за одно пересечение. Однако это не приводит к правильным результатам в случаях, когда с вершинами пересекаются строки 1, 7, 9 или 11. Вводят локальные минимумы и максимумы (считаются за два пересечения), а остальные учитываются как одно пересечение. Локальный минимум - Y-координаты предыдущей и последующей вершин больше, чем у рассматриваемой вершины. Аналогично определяется локальный максимум. На сканирующих строках 1 и 7 локальные минимумы, на строках 9 и 11 — локальные максимумы. Убедиться, что такие промежуточные вершины пересекаются только один раз, довольно легко: одно из смежных ребер укорачивается до того, как вычисляются пересечения (рис. 11.26).

Такое укорачивание проводится только в том случае, если вершина лежит на сканирующей строке, что случается всегда, когда координаты вершин — целые числа, и редко, если координаты вершин представлены с более высоким разрешением, чем сама растровая сетка.