Математическая модель процесса всасывания шестеренного насоса с внешним зацеплением

Рабочая жидкость, которая попадает из полости всасывания в межзубовую впадину, вращается вместе с шестерней с угловой скоростью 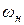. Центробежная сила, которая действует на жидкость, стремится выбросить ее из впадины и препятствует заполнению рабочей камеры. Сопровождает это явление снижение давления в зоне донышек впадин шестерен ниже давлению на входе насоса, что может привести к кавитации жидкости с ее кипением и выделением растворенных газов. Парогазовая смесь также препятствует полному заполнению межзубовых впадин.

Давление жидкости, необходимое для обеспечения эффективной работы шестеренного насоса, определим из уравнения баланса сил, которые действуют на жидкость в межзубовой впадине шестерни.

На элементарную частицу жидкости 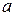в форме параллелепипеда высотой 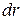, длиной 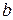и шириной 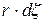действуют в радиальном направлении силы давления жидкости 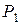и и 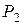центробежная сила 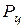(рис. 8.7). Приняв направление действия силы от центра вращения шестерни за положительное, можно записать уравнение равновесия частицы жидкости

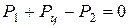. (8.8)

Указанные силы определяются зависимостями

;

;

,

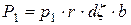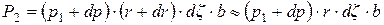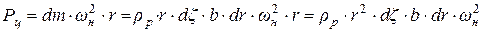где 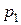- давление жидкости на ближнюю к центру вращения шестерни грань параллелепипеда 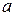, который отстает от центра 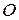на расстоянии (радиусе) ;

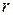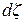- центральный угол охвата параллелепипеда ;

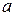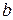- ширина шестерни;

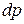- приращение давления жидкости на высоте ;

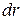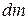- элементарная масса частицы жидкости ;

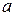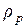- плотность рабочей жидкости.

При определении силы 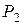принято допущение, что площадь 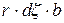ближнего к центру вращения шестерни грани параллелепипеда 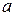равняется площади 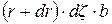дальней от центра вращения шестерни грани.

Подставив полученные зависимости в уравнение (8.8), имеем

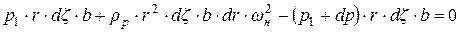. (8.9)

После превращения (8.9) принимает вид

,

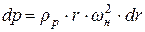откуда после интегрирования

.

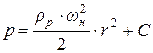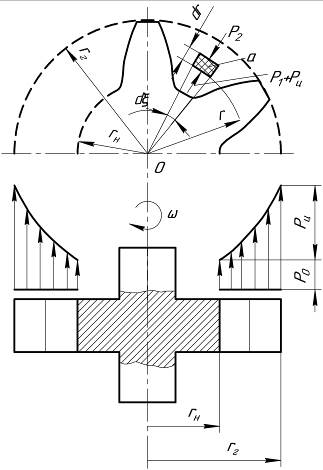
Рис. 8.7. Схема действия сил на рабочую жидкость в полости всасывания

Постоянную интегрирование 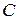определим, приняв, что давление на донышке впадины шестерни 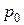имеет место при значении текущего радиуса 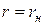(радиус окружности ножек зубьев). Тогда постоянная интегрирование равняется

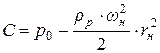. (8.10)

Зависимость давления жидкости во впадине шестерни от текущего радиуса 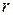, который изменяется в диапазоне 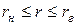( 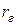- радиус окружности головок зубов), с учетом (8.16) имеет вид

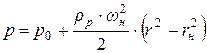, (8.11)

то есть давление во впадине шестерни изменяется по параболическому закону (рис. 8.7).

Давление на входе в межзубовую впадину шестерни (на радиусе 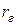окружности головок зубьев) имеет максимальное значение

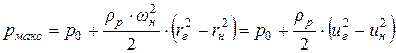, (8.12)

где 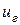и 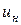- линейные скорости на радиусах соответственно 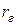и .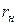

Вторая составляющая правой части уравнения (8.11) является давлением жидкости, обусловленным действием центробежных сил. Максимальное значение это давление имеет на входе в межзубовую впадину, то есть в соответствии с (8.12) равняется

.

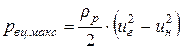Для надежного и полного заполнения жидкостью рабочих камер (межзубовых впадин) необходимо, чтобы давление во всасывающем пространстве превышало давление на входе в межзубовые впадины шестерни 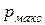, определяющая составляющая которого обусловливается величиной давления 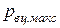. Крайним случаем недозаполнения межзубовых впадин является полное прекращение питания шестерного насоса и его холостая работа.

Для предотвращения недозаполнения рабочих камер жидкостью в полости всасывания ограничивают угловую скорость вращения шестерен 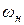и повышают давление жидкости во всасывающем пространстве за счет уменьшения гидравлических потерь или использования бустерных (вспомогательных) нагнетателей.