Подача шестеренных насосов с внешним зацеплением и ее равномерность

Как следует из приведенной физической модели (раздел 8.2.1), рабочий процесс шестеренных насосов отличается значительной сложностью по сравнению с рабочим процессом насосов других конструкций.

Для определения средней идеальной подачи шестеренного насоса с внешним зацеплением физическую модель его рабочего процесса можно представить как процесс переноса жидкости из полости нагнетания в полость всасывания впадинами обеих шестерен одинаковых размеров при условии равенства объема впадины объему зуба. При таком подходе рабочий объем насоса определяется объемом кольца со средним диаметром 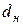, радиальной высотой, ровной высоте зуба 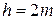и шириной 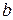[ 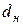- диаметр начальной (делительной) окружности, 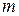- модуль зацепления, 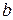- ширина шестерен] (рис. 8.6, а), то есть

. (8.1)

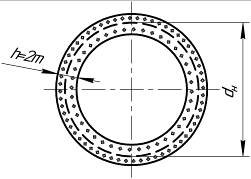
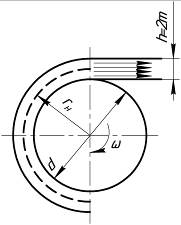
а) б)

Рис. 8.6. Принципиальная схема к упрощенной физической модели рабочего процесса шестеренного насоса с внешним зацеплением

Средняя идеальная подача шестеренного насоса с внешним зацеплением, исходя из (8.1), равняется

, (8.2)

где 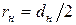- радиус начальной окружност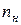и;

и 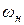- частота вращения и угловая скорость вращения шестерен.

Среднюю подачу шестеренного насоса с внешним зацеплением можно отождествить с потоком (струей) жидкости, который, вращаясь совместно с барабаном диаметром 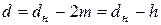, отрывается от него в гибком канале высотой 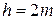и шириной 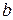(рис. 8.6, б).

Учитывая, что 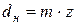( 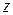- число зубьев в шестерне), выражение (8.2) можно представить следующим образом

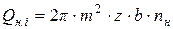. (8.3)

Экспериментально определенная средняя подача шестерного насоса с внешним зацеплением несколько превышает аналитически рассчитанную по уравнениям (8.2) и (8.3), что свидетельствует о превышении суммы объемов впадин двух шестерен над суммой объемов их всех зубьев. При количестве зубьев 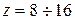в шестернях экспериментально определенная и аналитически рассчитанная подаче насоса практически не отличаются при условии замены в формулах значения 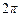эмпирическим коэффициентом 6,5. Поэтому рекомендуется [2] для насосов с числом зубьев в шестернях 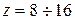определять среднюю идеальную подачу формулами

.

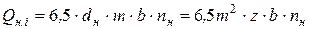Текущая подача шестеренных насосов с внешним зацеплением отличается ощутимой неравномерностью, но получение зависимости текущей подачи от угла поворота шестерен связано с громоздкими специфическими изложениями [40]. Поэтому ограничимся выведением формул для величины мгновенной подачи насоса при нескольких характерных значениях углов поворота шестерен.

В качестве допущений принимаем, что длительность зацепления шестерен (коэффициент перекрытия) равняется единице, шестерни имеют одинаковые числа зубьев, зацепление нормальное эвольвентное.

В общем случае текущая подача шестеренного насоса с внешним зацеплением определяется зависимостью (рис. 8.2, а, б)

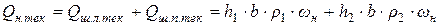, (8.4)

где 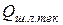и 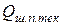- расход жидкости, которая вытесняется в нагнетательный патрубок поверхностями зубьев соответственно левой (ведущей) и правой (ведомой) шестерен;

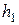и 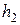- текущие рабочие высоты зубьев соответственно левой и правой шестерен;

и - текущие расстояния от центров вращения соответственно левой и правой шестерен к центрам тяжести проекций на радиальную плоскость каждой шестерни рабочих поверхностей зубов.

При положении точки зацепления 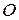зубьев 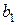и 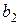на горизонтальной оси симметрии левой и правой шестерен (рис. 8.2, а) имеют место соотношения

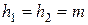и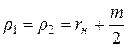

с учетом которых выражение (8.4) принимает вид

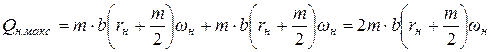, (8.5)

и в этом случае текущая подача шестерного насоса имеет максимальное значение.

При положении шестерен, которое отвечает началу или окончанию (рис. 8.2, б)зацепления зубьев 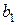и 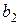, текущие соответствующие параметры будут иметь значение:

- в начале зацепления

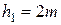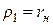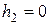и , и ;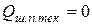

- по окончанию зацепления

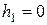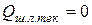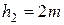и , и .

В этих положениях шестерен текущая подача шестерного насоса имеет минимальное значение, которое равняется

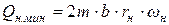. (8.6)

Таким образом, во всех промежуточных, кроме рассмотренных, положениях шестерен текущая подача насоса имеет значение 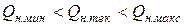, то есть имеет пульсирующий характер и является периодической функцией с периодом, ровным 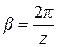. За один оборот шестерен происходит число колебаний подачи, которое равняется числу зубьев.

Амплитуда колебаний подачи шестерного насоса определяется разницей между максимальной (8.5) и минимальной (8.6) подачами

.

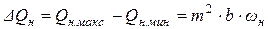Среднее арифметическое значение текущей подачи шестерного насоса может быть определено по зависимости

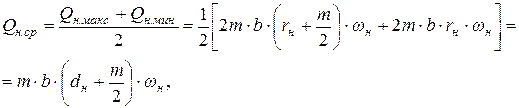(8.7)

или при условии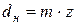

.

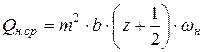Таким образом, текущая подача шестеренных насосов с внешним зацеплением определяется лишь параметрами зацепления и не зависит от объемов впадины и тела зуба.

Неравномерность подачи шестеренных насосов с цилиндрическим эвольвентным зацеплением при коэффициенте перекрытия 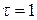оценивается коэффициентом неравномерности

.

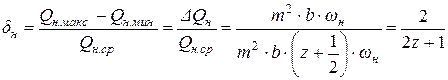Фактическая неравномерность подачи шестеренного насоса значительно превышает (до 2÷3 раз) расчетную из-за внутренних объемных утечек жидкости (обратного потока жидкости из полости нагнетания в полость всасывания через часто недозаполненные рабочие камеры). Неравномерность подачи увеличивается с увеличением значения коэффициенту перекрытия 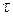и уменьшается с увеличением числа зубьев 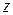(например, при использовании шестерен, которые состоят из двух, смещенных одна относительно другой на угол 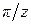, половин [2]).

Расчетная и фактическая неравномерность подачи шестеренных насосов с внешним зацеплением значительно превышает неравномерность подачи объемных насосов других типов.