Описание установки и вывод рабочей формулы. Определение момента инерции махового колеса методом колебаний производят следующим образом

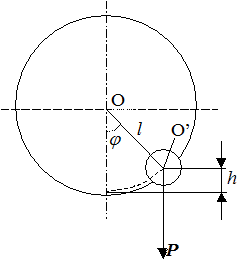
Рис. 1.

Определение момента инерции махового колеса методом колебаний производят следующим образом. К ободу колеса прикрепляют некоторый груз весом Р (рис.1). Колесо выводят из положения равновесия и затем отпускают. Система начинает совершать колебания, которые при достаточно малых углах отклонения можно считать гармоническими. Так как ось вращения проходит через центр тяжкести колеса, то при отклонении груза от положения равновесия потенциальная энергия системы равна потенциальной энергии груза Р , поднятого на высоту h:

W_пот=mgh, (7)

где m- масса груза. При прохождении положения равновесия эта энергия полностью переходит в кинетическую энергию колеса и груза. Следовательно, можем записать

W_kин=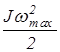

где J- момент инерции всей системы относительно оси вращения О, - угловая скорость системы в момент прохождения положения равновесия.

Запишем закон сохранения энергии

mgh= 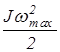. (8)

Так как h и непосредственно измерить трудно, выразим их через другие измеряемые величины. Из рис.1. видно, что

h=L(1-cos 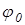)=2L sin²

Синусы малых углов можно заменять самими углами в радианах, поэтому sin² . Тогда . При гармонических колебаниях угловое смещение определяется формулой

sin ,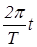

где 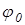-амплитуда колебаний; Т- период колебаний .Угловая скорость равна

cos .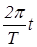

Подставляя выражения для h и амплитудного значения угловой скорости в (8), получим:

Т=2 . (9)

Эта формула определяет период физического маятника.

Момент инерции J системы равен сумме момента инерции колеса и момента инерции J₁ добавочного груза относительно оси вращения системы

J₁=J₀+J₁ (10)

Момент инерции груза относительно оси вращения системы согласно теореме Штейнера определяется так:

J₁=J₀₁+mL², (11)

где J_0l- момент инерции груза относительно оси О^/ , проходящей через центр тяжести груза, параллельно оси О; L- расстояние между осями.Если добавочный груз имеет форму цилиндра, геометрическая ось которого расположена параллельно оси О, то

J₀₁= 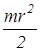, (12)

где r- радиус груза.

С учетом (10)-(12) уравнение (9) можно переписать в виде

Т²= 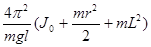. (13)

Из (13) находим момент инерции колеса

J₀= 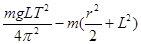. (14)

Для определения момента инерции махового колеса методом колебаний по формуле (14) необходимо измерить массу m и радиус r груза, расстояние L от центра тяжести груза до оси вращения и период гармонических колебаний колеса с грузом Т.

Порядок выполнения работы

1. Начертить в тетради таб. 1.

Табл.1

№ измерен.	m	n	t	Tср	L	r	J0
1. 2. 3. 4. 5.

2. Запустить программу 4К.ЕХЕ. Для этого указать курсором на 4К.ЕХЕ и щелкнуть левой кнопкой мыши (в дальнейшем эту команду обозначим L’ на 4К.ЕХЕ). Изучить информацию на экране.

3. Задать значения массы груза m, расстояния между осями L и радиус груза r.

4.L’ на команде «Обновить» 4.

5. Нажать левой кнопкой мышки на груз и не отпуская установить угол отклонения груза.

6. L’ на Начать.

7. L’ на Зафиксировать время 10 колбаний.

8. L’ на Зафиксировать время 20 колбаний.

9. Повторить пункты 5-8 еще 4 раза.

10. L’ на калькуляторе и вычислить значения Т₁₀, Т₂₀, Т_ср, J₀.

11. Вычислить средний момент инерции по формуле:

J_ср= .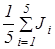

12. Вычислить абсолютную и относительную ошибки измерений.

13. Данные таблицы переписать в тетрадь.

14. Закрыть программу 4К.ЕХЕ.

Контрольные вопросы и задания.

1. Сформулируйте теорему Штейнера.

2. Приведите вывод рабочей формулы.

3. Как вычисляются моменты инерции цилиндра ?