Колебания полосового магнита в магнитном поле Земли

Подвесим полосовой постоянный магнит на очень тонкой нити в некотором магнитном поле. Поле создается каким-либо устройством или Землей.(в лабораторной работе используем магнитное поле Земли с индукцией B₀). Направление вектора индукции магнитного поля B₀ определяем по компасу. Численное значение его модуля нам может быть неизвестным. Ориентируем полосовой магнит по направлению вектора индукции магнитного поля B₀ (в условиях эксперимента ориентируем его северным концом к N). Дождемся, пока магнит перестанет колебаться. Затем осторожно отклоним его на малый угол g, не более нескольких градусов. На магнит станет действовать возвращающий момент M .В соответствии с уравнением (2.3)

M = – B₀ p_m sing, (6.1)

где p_m – магнитный момент полосового магнита. При малых углах g можно принять sing =g. Поэтому из (6.1) получим:

M = – B₀ p_m g . (6.2)

Запишем основное уравнение динамики вращательного движения

M = I e , (6.3)

где e – угловое ускорение магнита, равное

,

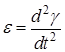I – момент инерции магнита относительно центра масс. I определяется формулой

, (6.4)

где m – масса магнита (определяется взвешиванием), с – длина магнита, b – ширина магнита (определяются измерениями).

Из уравнений (6.2) и (6.3) получим

I e = –B₀ · p_m g

,

.

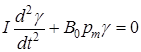Обозначим

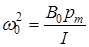. (6.5)

Тогда

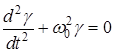. (6.6)

Получено линейное однородное дифференциальное уравнение второго порядка. Общее решение уравнения имеет вид

g = A cos(w t+ a) .

Следовательно, движение магнита представляет собой гармоническое колебание с периодом

.

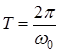С учетом (6.5) получим

.

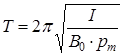Из этого уравнения найдем магнитный момент p_m

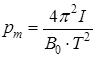. (6.7)

Момент инерции I определяется по уравнению (6.4), период колебаний магнита можно получить экспериментально. Численное значение индукции B₀ нам неизвестно. Для определения магнитного момента p_m воспользуемся уравнением (4.6) . По уравнению (5.1)

B₁=B₀ tgj .

Подставив это выражение в уравнение (4.6), получим

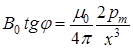, (6.8)

где x – расстояние от центра полосового магнита до оси стрелки компаса.Из этого уравнения следует

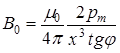. (6.9)

Подставив уравнение (6.9) в уравнение (6.7), получим искомый магнитный момент p_m:

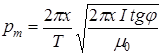. (6.10)

Из уравнения (6.10) следует, что для определения магнитного момента p_m полосового постоянного магнита необходимо вычислить по уравнению (6.4) момент инерции I магнита, период Т колебаний магнита в магнитном поле Земли, угол j отклонения стрелки компаса от магнитного меридиана.