Магнитное поле и его силовая характеристика. Закон Ампера

Определение магнитного момента полосового магнита

Магнитное поле и его силовая характеристика. Закон Ампера

Магнитное поле возбуждается движением электрических зарядов, то есть электрическими токами. Силовой характеристикой магнитного поля является вектор магнитной индукции B. В произвольной точке магнитного поля вектор B по направлению совпадает с направлением северного полюса бесконечно маленькой магнитной стрелки, имеющей возможность вращаться вокруг оси без трения. Модуль вектора Вможно определить по закону Ампера

dF=I·dl·B·sina , (1.1)

где dF – сила, действующая на элемент проводника длиной dl, по которому протекает ток I, a – угол между векторами dl и B.

Из этого уравнения найдем индукцию магнитного поля при a=p/2

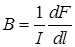(1.2)

Единица магнитной индукции – тесла (Тл).Найдем размерность магнитной индукции из уравнения (1.2):

,

[B]=M×T^-2×I^-1.

2. Контур с током, полосовой постоянный магнит и стрелка компаса в магнитном поле.

Пусть плоский контур с током помещается в однородное магнитное поле с индукцией B. По правилу буравчика выберем направление нормали n к плоскости контура (с конца вектора n ток I виден протекающим против часовой стрелки). Модуль единичного вектора nравен 1. При совпадении направлений векторов B и n (угол a между ними равен нулю) на контур вращающий момент М не действует. При возрастании угла a возрастает вращающий момент, стремящийся уменьшить угол a.. Опыты показали, что независимо от формы контура этот момент пропорционален модулю вектора B, произведению тока I в контуре, площади контура S и sina. Поэтому можно записать

М = – B·I·S·sina .

Величину

p_m = I·S (2.1).

называют магнитным моментом контура. Магнитный момент – величина векторная. Он по направлению совпадает с вектором n. Следовательно, из этих уравнений получим

p_m=I×S×n, (2.2)

М = –B·p_m·sina(2.3)

M= - [B,p_m] = - [B, p_m× n]. (2.4)

Магнитное поле полосового магнита и стрелки компаса определяется очень большим количеством круговых микротоков, нормали n к которым ориентированы параллельно друг к другу. Поэтому и для полосового постоянного магнита, и для стрелки компаса можно пользоваться уравнениями (2.3) и (2.4), В соответствии с ними стрелка компаса при отсутствии трения в опоре устанавливается вдоль магнитного меридиана Земли, а плоскость рамки с током стремится установиться перпендикулярно вектору B.

3..Закон Био-Савара-Лапласа. Индукция магнитного поля в центре кругового тока.

По закону Био-Савара-Лапласа каждый элементарный участок тока длины dl, направленный в ту сторону, в которую течет ток, создает магнитное поле, индукция dB которого в любой точке поля определяется формулой (3.1)

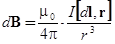, (3.1)

где m₀ - магнитная постоянная ( 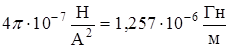; размерность [m₀] = L× M× T^-2× I^-2), r- радиус-вектор, проведенный от элемента проводника dl в точку М.

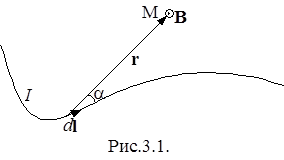
Вектор dB перпендикулярен плоскости, в которой лежат векторы dl и rи направлен так, что с конца вектора dB поворот вектора dl до совмещения с вектором r по кратчайшему пути виден происходящим против часовой стрелки.

Из уравнения (3.1) следует

, (3.2)

где a – угол между векторами dlи r. На рис.3.1 изображены проводник произвольной формы с током и вектор В индукции магнитного поля образованного элементом dl проводника в точке М пространства. Обозначение точки в центре круга означает, что вектор выходит из-за плоскости чертежа. Для нахождения индукции магнитного поля в точке пространства, созданного током всего проводника, необходимо проинтегрировать выражение (3.2) по всей длине проводника. При этом могут меняться величина радиус-вектора и угол a.

4. Индукция магнитного поля на оси кругового тока и полосового постоянного магнита.

Предварительно найдем индукцию B₁на оси кругового тока на расстоянии x от плоскости, в которой лежит контур (рис. 4.1)

Вектор dB определяем по закону Био-Савара-Лапласа (3.1), а его модуль – по уравнению (3.2). Так как векторы dl и r взаимно перпендикулярны, то sina в уравнении (3.2) равен 1.

. (4.1)

Из рис. 4.1 r2 = R2+x2.

Тогда из уравнения (4.1) получим

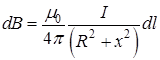. (4.2)

Из уравнения (4.2) видно, что векторы dB по модулю равны между собой при равных по длине элементах dl.

Поэтому равны все векторы dB_^, расположенные в плоскости, перпендикулярной оси x, а векторная сумма всех векторов dB_^равна нулю. Все векторы dB_||, расположенные по оси x, направлены одинаково и равны между собой.

Поэтому

.

Из уравнения (4.2) и двух последних уравнений получим:

,

,

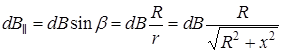. (4.3)

Площадь S₁, охватываемая контуром с током, равна.S = pR². Поэтому, с учетом (2.1), можно из (4.3) получить

. (4.4)

Единичная нормаль n к плоскости кругового тока I направлена по правилу буравчика (с конца вектора n ток I виден протекающим против часовой стрелки). Векторы B₁, p_m, n направлены одинаково. Из (4.4) получим

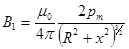. (4.5)

При x>>R можно пренебречь радиусом кругового тока R:

. (4.6)

Магнитное поле полосового магнита определяется очень большим количеством круговых микротоков, нормали n к которым параллельны друг к другу.

Поэтому для магнита также можно пользоваться уравнением (4.6), если x³3a, где a – длина магнита, а x – расстояние вдоль оси магнита, отсчитываемое от центра магнита.