Умножение двоичных чисел
Применительно к двоичной ПСС наиболее известны следующие основные способы выполнения операций умножения:
· умножение, начиная с младших разрядов множителя:
а) «ручной» метод:
1001— множимое,
* 0101 — множитель,
1001 – частичное произведение
 0000 частичные
0000 частичные
 + 1001 произведения,
+ 1001 произведения,

 0000
0000
0101101 – произведение;
б) «машинный» метод:
1001 — множимое,
*0101— множитель,
 1001
1001
+01001 частичные суммы,
+101101
+0101101 – произведение;
· умножение, начиная со старших разрядов множителя:
а) «ручной» метод:
1001 — множимое,
* 0101 — множитель,
 0000
0000
1001 частичные произведения,
0101101 - произведение;
б) «машинный» метод:
1001 - множимое,
0101 - множитель,
 0000
0000
+01001 частичные суммы,
+010010
+0101101 – произведение.
При «ручном» методе в обоих случаях умножение сводится к последовательному поразрядному умножению множимого на цифры множителя и накоплению (суммированию) получаемых частичных произведений. При этом операциями сложения могут управлять разряды множителя: если в i-м разряде множителя находится единица, то к сумме частичных произведений добавляется множимое с соответствующим сдвигом на i — 1 разряд (вправо или влево в зависимости от принятого способа выполнения операции умножения); если в i-м разряде множителя нуль, то множимое не прибавляется.
При «машинном» методе произведение формируется в виде возрастающего (по модулю) значения частичной суммы, равной после умножения на i-й разряд множителя сумме первых i частичных произведений.
Рассмотренные примеры показывают, что для получения произведения, помимо сложения, необходимо выполнять операции сдвига чисел (множимого либо частичной суммы). Очевидно, что произведение двух n-разрядных чисел есть число 2n-разрядное. Поэтому в случае ограничения поля цифр произведения n-разрядами при умножении целых чисел в качестве результата берутся младшие n разрядов (в старших n разрядах должны быть нули, так как в противном случае вырабатывается признак переполнения), а при умножении правильных дробей в качестве результата берутся старшие n-разрядов (младшие n разрядов отбрасываются — происходит усечение числа — либо используются для округления кода старших n разрядов).
Знак произведения формируется по известному правилу:
(+)•(+)=(+);
(+)•(-)= (-);
(-)•(+) = (-);
(-)•(-) = (+).
В ЭВМ знак «-» числа кодируется единицей, а «+» — нулем, но правило формирования знака сохраняется. Операция, которую реализует ЭВМ для определения знака произведения, называется суммой по модулю два и обозначается
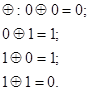
Алгоритм умножения чисел, представленных в форме с плавающей запятой, определяется следующим соотношением:
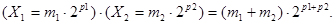
При реализации операции умножения над числами с плавающей запятой выделяют следующие этапы:
1) определение знака произведения путем сложения по модулю два знаков мантисс операндов;
2) перемножение модулей мантисс по правилам умножения дробных чисел с фиксированной запятой;
3) определение порядка произведения путем алгебраического сложения порядков сомножителей (с использованием дополнительного, обратного или модифицированного кодов);
4) нормализация результата (так как сомножители нормализованы, то денормализация возможна только на 1 разряд и только вправо) и округление мантиссы в случае необходимости.
Дата добавления: 2016-04-14; просмотров: 3031;
