Информационные технологии. Технология (от греч. techne –искусство, мастерство, умение) есть совокупность методов обработки, изготовления
Технология (от греч. techne –искусство, мастерство, умение) есть совокупность методов обработки, изготовления, изменения состояния, свойств, формы сырья, материала или полуфабриката, осуществляемых в процессе производства. Под информационной технологией (ИТ) обычно понимают совокупность методов, способов, приемов и средств обработки документированной информации, включая прикладные программные средства и регламентированный порядок следования их применений, а также совокупность всех видов информационной техники. ИТ ориентируются на получение, обработку и распространение информации.
Становление и развитие технологий стремительно изменяет окружающий мир. С самого начала эти процессы рассматривались в тесной связи с экономическими объектами, т.к. процесс всякой деятельности осуществляется по технологии, определяемой целью, предметом, средствами, характером операции и результатами.
Понятие «технологический процесс» в экономической литературе фактически было вытеснено термином «бизнес-процесс». Эти понятия во многом совпадают.
В основе описания бизнес-процессов лежат понятия:
· объект - информационный, материальный или финансовый, используемый в бизнес- процессе (оборудование, счет);
· событие – внешнее (не контролируемое в рамках процесса) действие, произошедшее с объектом (получение письма, поломка оборудования, начисление штрафа);
· операция – элементарное действие, выполняемое в рамках рассматриваемого бизнес-процесса (посылка письма, оплата счета);
· исполнитель – должностное лицо, ответственное за выполнение одной или нескольких операций бизнес-процесса (менеджер, сотрудник архива, директор).
Жизненный цикл объекта связан с внешними событиями и операциями, выполняемыми исполнителями в составе ПРОЦЕССА.
ИТ играют важную роль в поддержке бизнес-процесса. Они проникли во все виды деятельности человека, т.к. позволяют интегрировать различные виды технологий, синтезировать и накапливать информацию для внедрения в практику в соответствии с общественными потребностями. Целью широкого распространения ИТ является решение проблемы информатизации общества, понимаемой как распространение и внедрение комплекса мер, направленных на своевременное использование достоверной информации во всех сферах человеческой деятельности.
Арифметико-логические основы ЭВМ.
Позиционные системы счисления
Система счисления.
Система счисления — это совокупность цифровых знаков и правил их записи, применяемая для однозначной записи чисел. Все системы счисления подразделяются на позиционные и непозиционные.
Непозиционной называется такая система счисления, в которой значение цифры не зависит от ее положения в ряду цифр, изображающих число. Примером является римская система счисления, в которой для обозначения отдельных чисел используются буквы римского алфавита. Цифры в римской системе обозначаются различными знаками:
1 — I; 3 — III; 5 — V; 10 — X; 50 — L; 100 — С; 500 — D; 1000 — М. Запись числа осуществляется по каждый меньший знак, поставленный справа от прибавляется к его значению, а слева — вычитается из него: так, ХС — 90; СХ — 110; MCMLXXXVIII — 1988. Выполнять арифметические действия в непозиционных системах неудобно. Поэтому в настоящее время эти системы не используются для расчетов.
Позиционной называется такая система счисления, в которой значение цифры зависит от ее положения в ряду цифр, изображающих число, т. е. веса. В десятичной системе счисления вес каждой последующей цифры в 10 раз больше веса предыдущей. Например, цифра 2 в 1235 имеет значение 200, так как она в третьей справа позиции числа.
Позиционная система счисления (ПСС) характеризуется количеством различных цифр, используемых для записи чисел. Максимальное количество различных цифр, используемых для записи чисел в данной системе счисления, называется основанием системы счисления.
Любое число, записанное в р-ичной ПСС, может быть представлено в следующем виде:
 (2.1)
(2.1)
где  — любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме
— любая цифра (символ), используемая в данной ПСС из множества {0,1,..., р — 1}; n, … , m — номера разрядов числа; р — основание ПСС, которым может быть любое целое число, кроме 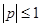 и
и 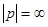 ;
;  — веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:
— веса разрядов. Например, число = 1235,87 по (2.1) имеет вид:
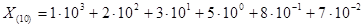
В ЭВМ применяют ПСС с недесятичным основанием: двоичную, восьмеричную, шестнадцатеричную и др.. В таблице показано соответствие записи чисел в десятичной, восьмеричной и шестнадцатеричной системах счисления.
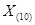
| 
| 
| 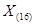
|
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F |
Двоичная ПСС получила самое широкое применение в ЭВМ благодаря следующим достоинствам.
1. Числовая информация в ЭВМ отождествляется с состоянием используемых двоичных физических элементов. В двоичной ПСС 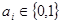 . Поэтому для физического представления
. Поэтому для физического представления  достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.
достаточно использования элементов с устойчивыми состояниями, кодируемыми 1 и 0. Например, транзистор может быть в открытом или закрытом состоянии, а следовательно, иметь на выходе высокое или низкое напряжение, ферритовый сердечник в устойчивом состоянии может иметь положительную или отрицательную остаточную магнитную индукцию, лампочка включена или выключена, отверстия на перфокарте пробиты или нет. Такие элементы принято называть двухпозиционными или двоичными. Очевидно, что реализация элементов, которые должны различать одно из двух состояний (0 или 1), оказывается проще и надежнее, чем реализация элементов, которые должны различать одно из 10 состояний.
2. Арифметические операции выполняются наиболее просто. Например, таблицы сложения и умножения одноразрядных двоичных чисел имеют соответственно вид:
0 + 0 = 0; 0 * 0 = 0;
0 + 1 = 1; 0 * 1 = 0;
1 + 0 = 1; 1 * 0 = 0;
1 + 1 = 10; 1 * 1 = 1.
3. Процесс синтеза схем ЭВМ упрощен, так как обозначение переменных и функций в используемом математическом аппарате алгебры логики, принимающих два значения 0 или 1, совпадает с двоичными цифрами.
В то же время громоздкость записи чисел в двоичной ПСС и трудность их восприятия человеком (см. табл.) приводит к необходимости перевода исходных данных (чисел) из десятичной системы счисления в двоичную, а результатов — из двоичной в десятичную. Эти переводы осуществляются в ЭВМ автоматически по определенным программам.
В соответствии с формулой (2.1) числа в разных ПСС можно представить следующим образом:
 (2.2)
(2.2)
Следовательно, в общем виде задачу перевода числа из ПСС с основанием  в ПСС с основанием
в ПСС с основанием 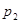 , формулируемую в виде:
, формулируемую в виде:
 (2.3)
(2.3)
можно представить как задачу определения коэффициентов  нового ряда, изображающего число в ПСС с основанием
нового ряда, изображающего число в ПСС с основанием 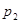 .
.
Решение (2.3) непосредственно в виде (2.2) осуществляют при «ручном» способе перевода чисел из одной ПСС в другую. Для «машинной» реализации перевода применяют следующие методы.
Метод деления.
Метод деления. Для перевода целого числа из десятичной системы счисления в любую другую ПСС необходимо разделить десятичное число на основание новой системы счисления, затем полученное частное снова разделить на основание новой системы счисления и так до тех пор, пока в частном не останется число меньше основания новой системы счисления ( 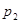 ) .Число в новой системе счисления запишется в виде остатков от деления, начиная с последнего частного, представляющего собой старшую цифру числа.
) .Число в новой системе счисления запишется в виде остатков от деления, начиная с последнего частного, представляющего собой старшую цифру числа.
ПРИМЕР:

Решение:
_1967 | 8
16 _245 | 8
_ 36 240 _30 | 8 Ответ:
 32 5 24 3
32 5 24 3 
_ 47 6
40
Метод умножения.
Метод умножения. Для перевода правильной десятичной дроби в другую систему счисления необходимо дробную часть десятичного числа последовательно умножать на основание новой системы счисления, представленное в исходной ПСС, до тех пор, пока в дробной части не останутся нули или не будет достигнута заданная точность перевода. В результате выполнения каждой операции умножения формируется одна цифра нового числа (начиная со старшей), равная целой части очередного произведения. Рассмотрим на примерах.
 ПРИМЕР 1.
ПРИМЕР 1.
0,125(10)=Х(2)
Х(2)-?
Решение:
0,125
* 2 Ответ: 
0,250
* 2
0,500
* 2
1,000
Неправильные дроби десятичной системы счисления в любую другую переводятся в два приема: целая часть переводится по одному правилу, дробная — по другому. Затем целую и дробную части числа записывают вместе, отделяя запятой.
ПРИМЕР:

Решение: 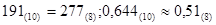
Ответ: 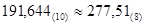
Перевод чисел в десятичную ПСС из любой другой ПСС удобнее всего производить, представляя эти числа в развернутой форме (2.1):
1101001(2)=1*26+1*25+0*24+1*23+0*21+1*20=64+32+0+8+0+0+1=105(10)
Правила перевода восьмеричных и шестнадцатеричных чисел в двоичные и наоборот исключительно просты, поскольку основания восьмеричной и шестнадцатеричной систем счисления есть целые степени числа (8=2а; 16=24).Для перевода восьмеричного (шестнадцатеричного) числа в двоичную форму достаточно заменить каждую цифру этого числа трехразрядным (четырехразрядным) двоичным числом.
При переводе из двоичной в восьмеричную (шестнадцатеричную) систему поступают следующим образом: двигаясь от запятой влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем каждую группу из трех (четырех) разрядов заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Заметим, что восьмеричная и шестнадцатеричная ПСС непосредственно не используются в ЭВМ для реализации операций, а служат лишь для облегчения чтения и записи человеком-оператором «машинных» кодов и широко используются в технике программирования. Очевидно, что самой удобной для человека является десятичная ПСС, а для машины — двоичная. Рассмотренные методы перевода чисел из одной 11СС в другую (делением и умножением) при реализации требуют существенных временных или аппаратных затрат. Для преодоления этого пользуются простым и оригинальным приемом: предварительно в двоичную ПСС переводят не все число, а только его цифры — в результате получается некоторая смешанная двоично-десятичная система.
Двоично-десятичное число образуется следующим образом: каждая цифра десятичного числа заменяется четырехразрядным двоичным числом — тетрадой.



 Например:
Например: 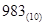

____ ____ ____ ____ ____
1001 1000 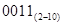 0110
0110 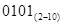
При обратном преобразовании необходимо каждую тетраду заменить эквивалентной ей десятичной цифрой.

 Например: 0111 0010
Например: 0111 0010 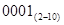


Дата добавления: 2016-04-14; просмотров: 904;
