Экспериментальные факты. Рассмотрим следующий эксперимент (рис

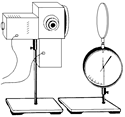Рис. 22.1

Рассмотрим следующий эксперимент (рис. 22.1). Электроскоп с прикрепленной к нему цинковой пластиной освещается светом от электрической дуги (этот свет содержит в своем спектре как видимое, так и ультрафиолетовое излучение).

Опыт 1. Электроскоп заряжен отрицательно. В этом случае под действием света он быстро разряжается.

Опыт 2. Электроскоп заряжен положительно. Свет не оказывает на электроскоп никакого действия.

Опыт 3. Электроскоп заряжен отрицательно, но между источником света и цинковой пластиной помещают обыкновенное стекло, которое, как мы знаем, не пропускает ультрафиолетовые лучи. Результат: свет не оказывает воздействие на пластину при любой сколь угодно большой освещенности.

Эти три опыта приводят к следующим выводам: 1) свет «вырывает» из металла электроны; 2) если пластина заряжена отрицательно, то электрическое поле пластины отталкивает вырванные электроны, и они улетают прочь, а пластина при этом разряжается; 3) если пластина заряжена положительно, то «выскочившие на свободу» электроны тут же возвращаются электрическим полем пластины обратно, заряд пластины при этом не меняется; 4) вырывать электроны из цинка «умеют» только ультрафиолетовые лучи.

Описанное явление – вырывание электронов из вещества под действием света – называется фотоэффектом.

Для более детального анализа этого явления рассмотрим следующий опыт (рис. 22.2).

Рис. 22.2

В стеклянный баллон, из которого выкачан воздух, помещаются два электрода. Внутрь баллона на один из электродов свет падает через «окошко» из кварцевого стекла, пропускающего ультрафиолет. Напряжение на электродах можно менять и измерять вольтметром.

К освещаемому электроду присоеди­няют отрицательный полюс батареи. Под действием света этот электрод испускает электроны, которые при движении в элект­рическом поле образуют электрический ток. При малых напря­жениях не все вырванные светом электроны достигают другого электрода. Если, не меняя интенсивности излучения, увеличи­вать разность потенциалов между электродами, то сила тока на­растает. При некотором напряжении она достигает максималь­ного значения, после чего перестает увеличиваться (рис. 22.3). Максимальное значение силы тока I_н называется током насыще­ния.Ток насыщения определяется числом электронов, испущен­ных за 1 с освещаемым электродом.

Рис. 22.3

Изменяя в этом опыте интенсивность излучения, удалось установить, что количество электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально по­глощаемой за это время энергии световой волны. В этом ни­чего неожиданного нет: чем больше энергия светового пучка, тем эффективнее его действие.

Теперь остановимся на измерении кинетической энергии (или скорости) электронов. Из графика, приведенного на ри­с. 22.3, видно, что сила фототока – электрического тока, вызываемого светом, отлична от нуля и при ну­левом напряжении. Это означает, что часть вырванных светом электронов достигает правого (см. рис. 22.2) электрода и при от­сутствии напряжения. Если изменить полярность батареи, то сила тока уменьшится, и при некотором напряжении U_зобратной полярности она станет равной нулю. Это значит, что электрическое поле тормозит вырванные электроны до полной остановки, а затем возвращает их на электрод.

Величину U_з мы легко можем измерить. Спрашивается: можем ли мы по величине U_з определить кинетическую энергию (а затем и скорость) вырванных электронов?

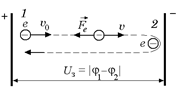Рис. 22.4

Если при «запирающем» напряжении U_з полностью отсутствует фототок, то это значит, что даже самые быстрые и «удачливые» электроны, вырванные из одного электрода, не смогли достичь другого.

Рассмотрим один такой электрон, который после вылета имел наибольшую скорость υ₀ и летел строго в направлении противолежащего электрода (рис. 22.4). Сила электрического поля 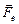на всем пути «тормозила» электрон и у самой цели (отрицательного электрода) повернула его назад. Эта сила совершила отрицательную работу А_е = –U_зе (здесь величина U_з – модуль запирающего напряжения, а е – модуль заряда электрона).

Применим теорему о кинетической энергии. В начале пути (положение 1) кинетическая энергия , в конце пути (положение 2) кинетическая энергия K₂ = 0. Тогда

DK = A_e Þ K₂ – K₁ = -U_зе Þ .

Мы получили важный результат:

. (22.1)

Поскольку т – масса электрона и е – заряд электрона – величины известные, а U_з можно измерить, то формула (22.1) позволяет нам определить максимально возможную скорость вырываемых из металла электронов. Но вот что удивительно: при увеличении интенсивности света, как показывают опыты, величина запирающего напряжения не меняется. А это значит, что не меняется и кинетическая энергия вылетающих электронов. Это очень странно. Ведь если свет – это электромагнитная волна, которая действует на электроны, то почему же увеличение амплитуды этой волны не вызывает увеличения скорости электронов?

Опыты дали еще один важный результат. Было обнаружено, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от интенсивности света. Если частота света меньше определенной для данного вещества минимальной частоты n_min, то фотоэффект не происходит.

Теория фотоэффекта

Объяснение фотоэффекта было дано в 1905 г. Альбертом Эйнштейном (1879–1955) – выдающимся физиком ХХ века. Он предположил, что свет излучается и поглощается отдельными порциями (квантами). Энергия каждой такой порции пропорциональна частоте

E = hn, (22.2)

где h – коэффициент, получивший название постоянной Планка, в честь выдающегося немецкого физика Макса Планка (1858–1947). Экспериментально установленная величина постоянной Планка равна h = 6,63×10^–34 Дж×с. Таким образом, электрон может получить от кванта света только четко определенную энергию E = hn – ни больше, ни меньше!

Заметим, что для того чтобы электрон вылетел из металла, над ним надо совершить определенную работу – так называемую работу выхода А_в. Поэтому энергия E = hn, переданная квантом света электрону, расходуется на совершение работы выхода и сообщение электрону кинетической энергии :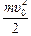

. (22.3)

Это уравнение называется уравнением Эйнштейна для фотоэффекта.

Читатель: Из формулы (22.3) следует, что скорость любого электрона, вырываемого из металла, должна быть одна и та же. Так ли это?

Автор: Не совсем. Не все электроны вырываются светом с самой поверхности, некоторых «вытаскивают» из глубины, и для таких «глубинных» электронов работа выхода должна быть несколько больше. В формуле (22.3) А_в – это работа по вырыванию самых «доступных» электронов, а υ₀ – скорость именно таких электронов.

Уравнение Эйнштейна объясняет основные факты, касающиеся фо­тоэффекта. Интенсивность света, по Эйнштейну, пропорци­ональна числу квантов (порций) энергии в световом пучке и поэтому определяет число электронов, вырванных из металла. Скорость же электронов согласно (22.3) определяется только частотой света и работой выхода, зависящей от рода металла и состояния его поверхности. От интенсивности света она не за­висит.

Для каждого вещества фотоэффект наблюдается лишь в том случае, если частота n света больше минимального значения n_min. Ведь чтобы вырвать электрон из металла даже без сооб­щения ему кинетической энергии, нужно совершить работу выхода А_в. Следовательно, энергия кванта должна быть больше этой работы:

hn > А_в.

Предельная частота n_min выражается так:

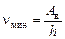. (22.4)

Этой частоте соответствует длина волны

. (22.5)

Эта величина называется красной границей фотоэффекта: если длина волны падающего света больше l_макс, то фотоэффекта не будет, а если меньше, то будет.

В таблице 22.1 приведены значения работы выхода для некоторых материалов. Для цинка красной границе соответствует длина волны l_макс = 3,7×10^–7 м (ультрафиолетовое излучение). Именно этим объясняется опыт по прекращению фотоэффекта с помощью стеклянной пластинки, задерживающей ультрафиолетовые лучи.

Таблица 22.1	У щелочных металлов работа выхода, напро­тив, меньше, а длина волны lмакс, соответствующая красной границе, больше. Так, для натрия lмакс =6,8×10–7 м. Читатель: Мне только непонятно, как чисто практически можно определить, во-первых, постоянную Планка, а во-вторых, работу выхода для данного металла.
Материал	Ав, эВ
Вольфрам Калий Литий Оксид бария Платина Серебро Цинк	4,5 2,2 2,4 1,0 5,3 4,3 4,2

Автор: Подставим в формулу (22.3) значение и получим hn = А_в + U_зе. Выразим отсюда U_з:

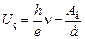. (22.6)

Если мы проведем ряд экспериментов по облучению данного металла светом разных частот и измерим соответствующие запирающиеся напряжения U_з, то можно будет построить график U_з = = U_з(n), который согласно формуле (22.6) будет прямой линией (рис. 22.5). (Ясно, что для разных металлов это будут разные прямые.)

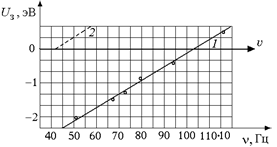Рис. 22.5

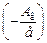Угловым коэффициентом этой прямой будет величина , а свободным членом , и эти значения можно вычислить по графику. После этого вычислить h и А_в не составляет труда.

СТОП! Решите самостоятельно: А1, В1, С1–С3.

Задача 22.1. Работа выхода электронов для натрия равнаА_вых = = 2,27 эВ. Найти красную границу фотоэффекта для натрия.

 

Авых = 2,27 эВ	Решение. Переведем значение работы выхода из электронвольтов в джоули: Авых = 2,27 эВ = 2,27×1,6×10–19 Дж » 3,63×10–19 Дж.
lмакс = ?

Воспользуемся формулой (22.5)

l_макс = м.

Ответ: l_макс = м.

СТОП! Решите самостоятельно: А2–А5.

 

Задача 22.2. Наибольшая длина волны света, при которой, происходит фотоэффект для вольфрама, 0,275 мкм. Найти работу выхода электронов из вольфрама; наибольшую скорость электронов, вырываемых из вольфрама светом с длиной волны 0,18 мкм; наибольшую энергию этих электронов.

 

lмакс = 0,275 мкм = = 0,275×10-6 м l = 0,18 мкм = = 0,18×10-6 м	Решение. Работа выхода электронов = » » 7,2×10–19 Дж. Из уравнения Эйнштейна для фотоэффекта, учитывая, что n = c/l, имеем
Ав = ? υмакс = ? Wмакс = ?

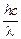= A_в + ,

откуда макси­мальная кинетическая энергия

W_макс = – А_в

= – 7,2×10^–19 Дж » 3,9×10^–19 Дж.

Зная наибольшую энергию вылетевших электронов, най­дем соответствующую ей наибольшую скорость:

υ_макс = » 9,3×10⁵ м/с.

Ответ: »7,2×10^–19 Дж; W_макс – А_в » 3,9×10^–19 Дж;

υ_макс = 9,3×10⁵ м/с.

СТОП! Решите самостоятельно: А6, В2, В3, С4.

Задача 22.3.Красная граница фотоэффекта у лития 520 нм. Какую обратную разность потенциалов (задерживающее напряжение) нужно приложить к фотоэлементу (к фотокатоду подключается плюс, к аноду-коллектору – минус источника напряжения), чтобы задержать электроны, испускаемые литием под действием ультрафиолетовых лучей длиной волны 200 нм?

 

lмакс = 520 нм l = 200 нм	Решение. Для красной границы фотоэффекта (волна с длиной lмакс­) справедливо . (1)
Uз = ?

Для длины волны l = 200 нм запишем уравнение Эйнштейна

= A_в + . (2)

Согласно формуле (22.1)

= eU_з. (3)

Подставим (1) и (3) в (2) и получим

= + eU_з Þ U_з = .

Подставим численные значения (все вычисления проводим в СИ):

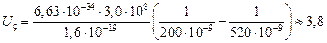В.

Ответ: U_з = 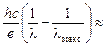3,8 В.

СТОП! Решите самостоятельно: А8, В4, В5, С5, С6.

 

<1234567>

---

Дата добавления: 2016-04-11; просмотров: 3178;

---