На какой угол призма отклоняет луч?
Рассмотрим призму с малым преломляющим углом j (рис. 6.3) и абсолютным показателем преломления п. Пусть на боковую грань призмы падает из воздуха луч под малым углом падения a.
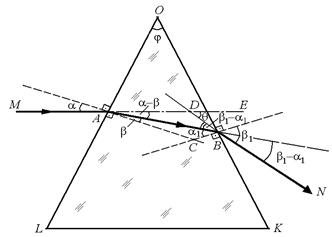 Рис. 6.3
Рис. 6.3
Читатель: А что значит «малым»?
Автор: Под «малыми» углами в этом параграфе мы будем понимать такие углы, для которых справедливо равенство sina » a.
Наша задача найти угол q между лучом, падающим на призму, и лучом, вышедшим из призмы (см. рис. 6.3). Рассмотрим внимательно рисунок. Луч МА входит в призму в точке А и после преломления на боковой грани ОL идет в направлении АВ. Угол падения луча a, угол преломления b. При этом после первого своего преломления луч отклоняется от своего первоначального направления на угол a – b.
Дойдя до второй грани призмы OK луч испытывает второе преломление в точке В и выходит наружу. Угол падения луча a1, а угол преломления b1. После этого преломления луч еще раз отклоняется к основанию, в этот раз на угол b1 – a1.
Таким образом, общее отклонение луча от первоначального направления будет
q = (a – b) + (b1 – a1). (6.1)
В этом можно убедиться из чисто геометрических соображений. Рассмотрим продолжение падающего луча АЕ и продолжение луча, вышедшего из призмы, DB. Угол между ними q = ÐBDE – это и есть угол отклонения луча от первоначального направления.
Из треугольника ADВ видно, что ÐBDE является его внешним углом, поэтому он равен сумме двух других углов треугольника, не смежных с ним. Получаем то же выражение для угла q = (a – b) + + (b1 – a1).
В четырехугольнике АОСВ два угла (ÐОАС и ÐОВС) – прямые, а сумма всех углов четырехугольника равна 360°. Поэтому:
j + 90° + 90° + ÐАСВ = 360° Þ ÐАСВ = 180° – j. (1)
С другой стороны, сумма углов DАВС равна 180°, тогда
b + a1 + ÐАСВ = 180°. (2)
Подставляя (1) в (2), получим
b + a1 + 180° – j = 180° Þ b + a1 = j. (3)
Запомним:
j = b + a1. (6.2)
Теперь воспользуемся законом преломления. Поскольку все углы здесь малые, то sina » a, sinb » b, sina1 » a1, sinb1 » b1, тогда
a = bп, (4)
b1 = пa1. (5)
Осталось выразить искомый угол g отклонения луча q через преломляющий угол призмы j и показатель преломления п. Для этого преобразуем равенство (6.1), учитывая, что q = b + a1 и используя равенства (4) и (5):
q = (a – b) + (b1 – a1) = (a + b1) – (b + a1) =
= (bп + пa1) – (b + a1) = п(b + a1) – (b + a1) =
= (п – 1)(b + a1) = (п – 1)j.
Итак, мы получили важную формулу
q = j(п – 1). (6.3)
Она устанавливает связь между преломляющим углом призмы j, показателем преломления призмы п и углом отклонения луча q. При этом оказывается, что угол отклонения q не зависит от угла падения a!
Читатель: А если луч падает на призму не из воздуха, а, например, из воды?
Автор: В этом случае п в формуле (6.3) – это относительный показатель преломления материала призмы относительно среды, в которой находится призма.
СТОП! Решите самостоятельно: А4, С1, D1, D4.
Задача 6.1. Луч света падает на стеклянную призму с показателем преломления 1,5. Угол падения при входе луча в призму 22°. Преломляющий угол призмы 41°. Определить угол преломления луча при выходе из призмы. На какой угол отклонится луч от первоначального направления, пройдя сквозь призму?
| n = 1,5 a = 22° j = 41° | Решение. В данном случае и угол падения a, и угол преломления j нельзя считать малым, поэтому расчет несколько усложняется (рис. 6.4). Будем проводить вычисления последовательно. 1. Рассмотрим первое преломление луча в точке А: |
| q= ? | |
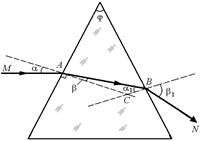 Рис. 6.4
Рис. 6.4
|
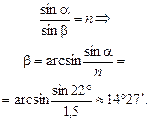
2. Воспользуемся формулой (6.2):
j = b + a1 Þ a1 = j – b = 41° – 14°27¢ » 26°33¢.
3. Рассмотрим второе преломление луча в точке В:
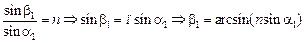 .
.
Подставляя уже полученное значение a1, получим
b1 = arcsin(n sina1) = arcsin(1,5×sin26°33¢) » 42°6¢ » 42°.
4. Осталось найти угол отклонения луча. Воспользуемся формулой (6.1):
q = (a – b) + (b1 – a1) = (22° – 14°27¢) + (42°6¢ – 26°33¢) » 23°.
Ответ: угол преломления луча при выходе из призмы 42°, угол отклонения луча от первоначального положения 23°.
Читатель: А если бы мы воспользовались приближенной формулой q = (п – 1)j?
Автор: Тогда мы бы получили q = (1,5 – 1)×41° » 20°30¢. То есть ошибка составила бы 2°30¢. Это, конечно, не очень много, но все-таки!
СТОП! Решите самостоятельно: В3, В4, С2, С3.
Дата добавления: 2016-04-11; просмотров: 5439;
